What If All User Interface (UI) Data Came In Reports?
As I've been trying to think more deeply about software application architecture, and experimenting with new ideas, one thing has become painfully obvious to me: shoehorning your domain model into your user interface (UI) leads to pain. Maybe not at first - maybe not when your user interface is a simplistic representation of your domain; but over time, as your user interface requirements evolve, your interface morphs from "representation" into "report". And, trying to pipe your domain model into a "report" is bad times. This is why I have a strong feeling that all user interface data should be compiled as, and delivered as, UI-specific reports.
To explore this idea, imagine that you have some sort of social media application in which you have a drop down menu full of friends:
| |
|
|
||
| |
 |
|
||
| |
|
|
At first, this seems straightforward - there's just some sort of list() method or getAll() method for friends. No problem! Domain model for the win!
But, as the application gets used, suddenly you realize that people have way too many friends. This drop down menu idea is no longer feasible. And so, you decide to have it filter down to only show best friends:
| |
|
|
||
| |
 |
|
||
| |
|
|
This is a slight hiccup; but, maybe it can be solved with some sort of filter flag, like list(isBestFriend=true). Sweet, problem solved!
At least for a little while. Because then you realize that people have way too many "best" friends as well. Suddenly, listing best friends leads to the same problem that became symptomatic when listing all friends. To solve this problem, you filter the drop down to be your "best best friends", but for convenience, show the user how many other best friends are being hidden from view:
| |
|
|
||
| |
 |
|
||
| |
|
|
Now we have a user interface that is fairly problematic. What the heck is a "best best friend?" How does the system distinguish between the favorability of one best friend over another? Perhaps this is based on some scheduled task that runs nightly and does a load of calculations? Perhaps it's based on the most recent shared communications? Perhaps this algorithm will change over time?
And what about that "View all 14 best friends," link? How do we get that? Do we have to pull back all best friends to get the count? Or, do we have to add some sort of getCount() method?
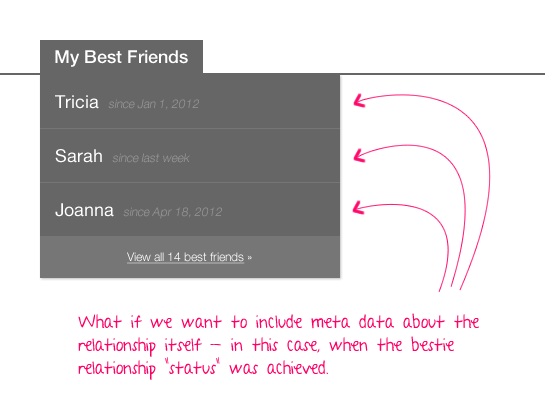
And, what if we wanted to provide some peripheral information about the friendship itself, such as when the best-friend status was achieved?
| |
|
|
||
| |
 |
|
||
| |
|
|
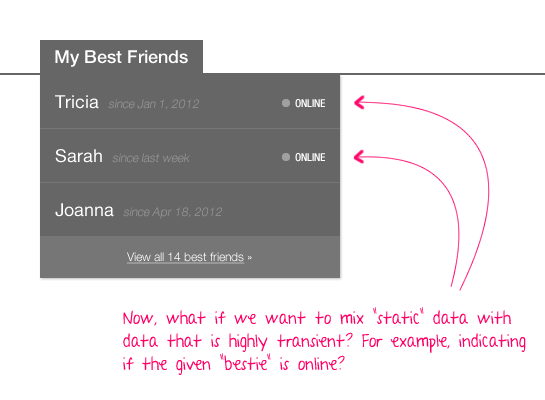
And, what if we then wanted to denote whether or not that given friend was currently online?
| |
|
|
||
| |
 |
|
||
| |
|
|
Is that really part of the "Friend" domain model at all? It's definitely not part of the concept of Friendship. Most likely, this is some sort of "UserSession" model that's completely disconnected from the idea of friendship altogether. So where do we get that? Do we have to query that information individually for each friend being returned in the list?
Slowly (or perhaps quickly), what seemed like a simple representation of your domain model has turned into this hodgepodge of domain / aggregate / transient data. The user interface is no longer a representation of your domain model - it's a report about the state of your application.
So, how to do we gather such a report? Maybe from something like this:
ui.partials.StandardLayout.getBestFriendDropdown( authenticatedUserID ) :: struct
This method doesn't return a domain model, or a collection of domain entities; this method returns a report that contains the data required specifically for the best friend drop down menu. The method internals are highly optimized for the report and may even use caching strategies that are targeted at that specific user interface.
Is this reusable? Absolutely not. Will you ever have another user interface that needs exactly this information? Most likely never. Doesn't this mean you have to create a lot of reports, especially if you have a really large application? Yes - a lot of highly optimized reports that leverage (in an encapsulated way) all the beneficial features provided by your particular persistance and caching implementation.
So anyway, those are some thoughts I've been having about software application architecture and about the responsibilities of data presentation. If anyone understands the pain I've been feeling, but has a completely different mitigation approach, I'd love to hear about it.

Reader Comments
I like to think that the frontend (the Js app) is a separate application. Thanks to that I don't have to clutter my domain (backend) with things that don't fit together (friendship and being online).
On the frontend app, the domain may actually have a different domain, where having friends being online (as part of the frontend domain) makes more sense.
I'm not sure if that's the best approach, though.
Nice post, inspired me to think more about this common problem!
Seems like a good illustration of why we use MVC architectures to separate the model and the view: views are interpretations of the model that are important to the user, and you can represent the same model data in different ways depending on what the user wants/needs.
It also points out, to me, how the model usually ends up being divided between two areas of concern. One concern being the management of the persistent data (beans, CRUD, validation, etc.), the other being the manipulation of the data (combining recordsets, performing calculcations) in support of the views and business rules particular to the application. The persistent data piece usually ends up being highly portable, able to be dropped into another application that uses the data for a different purpose, the other piece (more of a service piece) not quite so much.
And the view of course is highly specific to the app it serves.
I understand your pain Ben.
I have seen the problem arise that as the UI gets richer (or busier) then you run the risk of the rationally separated functionality of the model becoming much slower than it needs to be since you may have to go to several different objects to get the data which is visually related if not model related.
Unfortunately, I have no better way around the issue. The comments point out another challenge in that backend and frontend people draw hard lines between the two, sometimes to retain their sanity! but still, without taking a holistic approach, performance almost certainly will suffer. Do we really have to pick between performant apps and maintainable apps?
If it was easy, I guess we'd all be looking for work.
Hi Ben!
You mentioned "If anyone understands the pain I've been feeling, but has a completely different mitigation approach, I'd love to hear about it."
I don't know that it's a different approach, but I do think others have termed this "report" as a "view model", or a "presenter."
Sam
@Ben - Great post. I've definitely experienced your pain and I think you've brought up something good here. It's important to recognize that there are always different approaches to architecture. Every approach will have some sort of advantages and disadvantages. No implementation is perfect for all situations and it's always difficult to foresee what kind of impact your choices will have on future development. That said, you've given me something to think more deeply about. Thanks!
@Andrzej,
I haven't really gotten good at thinking about the front-end app as having a different domain model. Right now, I tend to just use plain-old JavaScript objects / arrays, to populate my front-end views. And, I'll use my front-end controllers to "augment" those data structures when needed by the particular view (ex. an "isSelected" boolean that is view-specific).
@Brian,
That's definitely where my mind is headed. I've been thinking a lot in terms of "commands" and "queries," which I touched on upon briefly in a previous post a little while back:
www.bennadel.com/blog/2438-Command-Query-Responsibility-Segregation-CQRS-Makes-Domain-Models-Practical.htm
Clearly, I am still formulating all of this stuff in my head. Sometimes, I think it makes complete sense; sometimes, I can't figure out how to wire any of it together.
@John V,
The scariest thing I've seen in some apps is that some domain model will get a "stat" attached to it - something like, "isHighPriority". This stat requires additional joins, maybe even a LEFT OUTER JOIN (yuck!!!), just to accomodate one of the views... then, the terrifying thing is, that view is eventually changed or discarded, but no know ever knows to remove that additional stat. So, it adds a burden, and for no reason at all :(
The way I'm thinking about the separation is that there is a core API that deals directly with the domain model. This is the truest representation of the application. You would execute your "commands" against this API.
Then, you would have "app specific" reports (or what I've been calling "partials") that could be namespaced by the type of app. Something like:
partials.desktop
partials.mobile
partials.api ( not the core api - an integration API )
Then, you could have a part of the application that is really involved with the domain; and, a number of other highly optimized, highly performant modules.
@Sammy,
I've heard of the "Presenter" approach, but I don't know that much about it. Mostly, I've heard of it in terms of the client-side code (in the context of a JavaScript application). I'll have to look into it more - thanks for the tip.
@Josh S,
Definitely the tradeoff in this "partials" approach would be duplication in "report" queries. The benefit, is that the domain model would remain very focused and would not be too hampered with performance concerns.
I know a lot of people shy away from "duplicate" queries; but, in my experience, it has not caused problems. Unless you are drastically changing the database schema, small changes may not even require many changes in the reports.
For example, let's say you add a new column to some table; the chances are, none of the existing report queries will actually need to be changed. Even removing a column can be easy - only affecting the UIs that were making use of that column.
@Ben: Just read the CQRS post. As I moved towards using objects to manipulate individual data records (first with Transfer, then with my own custom data access objects, soon with Hibernate), I still limited their use mainly to situations where I was only retrieving a single object (in order to perform CRUD operations). If I wanted to query multiple records for reports or to denote the current state of the application data overall, I'd still look to use queries for that.
That's still probably true for a lot of CFML developers given that A) database interaction through queries/SQL has always been a point of focus for CFML, and B) instantiating a large number of objects comes with a performance penalty. At this point, item B isn't as much of an issue, as object performance has improved, but if you can get what you need directly from the data in the database tables, why instantiate the records into objects?
For the developers working in object-heavy languages like Java, the idea of querying data and application state via a query rather than an array of objects might be something of a revelation, but not so much in CFML.
Ben, can you elaborate on this?
"LEFT OUTER JOIN (yuck!!!)"
@David,
Oh, I just mean that I prefer INNER JOINs over OUTER JOINs. I don't like the duality of a LEFT OUTER JOIN relationship - maybe it exists, maybe it doesn't. With INNER JOIN, something *has* to exist and it makes me happy :)
Plus, with an INNER JOIN, I can move the filtering in the join itself (ie. the ON clause), rather than having to move filtering into the WHERE clause.
That's all that I meant to insinuate :)
@Ben,
Hahahaha, that's extremely OCD. I like it.
@Brian,
I definitely still do a ton of querying. But, when Hibernate was added to ColdFusion, I saw a lot of people unsure (myself included) as to when to use ORM vs. when to use HQL vs. when to use straight-up SQL. I don't use a lot (much of any) ORM, so I still do a lot of SQL.
So, I guess the back-story is that I'm trying to get more into OOP and am trying to figure out how that fits into how I currently think about application development.
@David,
Ha ha ha, what can I say - I'm a fan of the INNER JOIN :D
@Ben: One of the benefits we get from using ORM objects over a row in a database recordset (beyond the built-in CRUD functions and relationship management) is the ability to define behavioral functions or computed properties that aren't persisted to the database.
Classic example: a Person ORM object with a getFullname() function that returns the combined value of the firstName and lastName properties that are retrieved from the database.
So if I needed to display a list of people for my UI, and I wanted to display each person's full name, it probably makes more sense to use HQL to retrieve that list since (I believe) the HQL can return the full name value as if it were a real database field...as opposed to looping through the data on the view page and having code on the view page combine the first and last name the way you want it.
(Aside: I guess you could argue that the getFullname() function accommodates/is tied to the UI in a way that mucks with the "purity" of the model, but I guess it depends on the situation)
But if I'm querying for a set of records that's purely persisted data from the database, then a plain old query is probably the easiest and most efficient way (performance-wise) to get it.
That's my take on it, anyway.
@Brian,
The "get full name" and the "get age" (given a date of birth) are the two most common use-cases I hear when it comes to weighing the pros/cons of queries vs. smarter objects.
I'm not sure how I feel about that kind of stuff. There's a lot of stuff in my user interfaces that seems purely UI-related. For example, imagine that I have a list of friends (in the above blog post), where I want to call out "new" friends in some way:
* Sarah
* Jan [NEW]
* Tracy
And, let's say the rule for this is any friendship that was formed in the last 7 days.
I could add that to a friend object:
friend.isNew()
... but my "app" doesn't really have a concept of "new". That's a requirement that is strictly part of my user interface. I may add it one day and remove it the next.
So, I wouldn't want it in the "business logic". I could put it in the client-side code (I've definitely rocked that before); or I could put it in a UI-oriented report.
.... so much to think about.
The people behind DCI - http://en.wikipedia.org/wiki/Data,_context_and_interaction are trying to solve this kind of problem.
In some contexts it may make sense to have friend.isNew() while in other contexts it shouldn't be even available to be called.
DCI is hard to achieve with most of the popular language. I'm just referencing to show the problem from another perspective.
@ben, i'm not sure how you can say IsNew() isn't in your "app" and would be "purely UI."
Imagine your "app" without any UI, essentially you've got an API at that point because otherwise what's the point. So in this scenario, not having IsNew() would make one less feature available right?
Something like the placement of your windows or size of your font is purely UI, anything dealing with data and how you get it to the user has to be considered part of the app IMO.
@John,
I guess I see the "is new" feature the same way you see fonts and window size. Imagine that you have two types of friends:
* Friend
* Best Friend
If you were going to output a list of both, you probably have some business-related flag for isBestFriend(). Ok, now imagine that "best" friends in the list are in a Gold font, and the regular friends are in the normal font.
I think we can agree that the Gold vs. Normal font is a UI-only matter - you wouldn't have a business property for isUsingGoldFont().
Well, I guess I see the "new" UI as very much akin to font color - it's a UI decoration that doesn't need extra settings in the business logic.
And, I guess, by that I mean that if I were to remove the "new" flag on the UI, the app itself would not have to change in any way. And, adding the "new" flag back in, the app wouldn't have to change either.
Now, I will definitely concede that if the logic was more "calculated", like, 15-days, but only weekdays, and not including holidays... then that WOULD be part of the business logic.
So, I guess my feelings on it are nuanced.
@Ben: I think, in the end, it all comes down to what implementation strikes the right balance of efficiency and practicality for the particular situation.
Using your example above, if you're only going to use this logic of who is "new" in that one UI, then maybe it makes sense to handle the "new" determination as part of the UI display of your list of friends, rather than putting that single-use logic in your model.
But if you think/realize you're going to use that "isNew()" logic in a couple of places, then it makes sense to put that logic somewhere so it can be utilized for those use cases. That "somewhere" is usually in the model if the logic returns pure data. If the reusable bit always comes with the same visual output, then maybe the "somewhere" should be a UI fragment/module; perhaps from a custom tag or UDF.
It's purely situational: there's no "one size fits all" approach.
In terms of a custom property that's purely a data transformation (like "getFullname()" or "getAge()"), here's an option worth considering: the persistent CFCs you create for ColdFusion ORM can extend another CFC (so long as THAT CFC isn't persisted). Put your custom property functions like getFullname() into that superclass, and let the ORM CFC focus solely on the persistent/database properties and relationships. That will let you keep the app-specific functions separate, and the ORM CFC could be moved to a different application if need be and attached to a different, app-specific superclass.
A few corrections/clarifications to some of the ideas I've posted here:
1. I didn't realize that you could subclass one ORM entity from another on a joined column, so my earlier statement about making sure the superclass isn't persisted is incorrect. But you can have an ORM CFC that is a subclass of a non-ORM CFC.
2. You wouldn't want to store values that are compositions or transformations of persisted properties into a non-persisted property (like a "fullName" property). You'd have to make sure such a property was updated every time someone changed the underlying persistent properties. Besides, if you're returning an array of entities via HQL you have access to whatever function you'd use to come up with the resulting value, and so you could just invoke the function as you looped through the array to generate your UI.
3. I forgot that HQL (despite it standing for "Hibernate Query Language") returns an array of Hibernate entities, not a query. And while that HQL array result can be converted to a query via EntityToQuery(), the query recordset does NOT include non-persistent properties (though it can include formula results from SQL-based calculations).
...Got a little carried away with the theory of how one might avoid having to transform the recordset data during the UI loop, and should've verified it worked in practice.
But hey, I learned a few things in the process. :)
And still, as long as the number of records/entities isn't so large as to cause performance issues, getting records for display as an array of ORM entities gives you the option of putting your transformative functions (like "getFullname()") into your entities (either in the ORM CFC itself or a superclass you can swap out) rather than in your display logic.
@Brian,
I would definitely conceded that if the is-new feature was used in a number of places, it would make sense to be part of the model itself. I always hate how NOT black and white this stuff is :D As someone who craves order and predictability, it is quite irksome :D
I should give ORM another look. I really have only looked at it from a technical standpoint - but not really done much trial and error with a real app.
@Brian (or Anyone else),
Totally off-topic from this post, but related to domain modelling. You seem like you've thought a good deal about domain modelling, so I wanted to get your thoughts on something. Imagine that I have a given set of data; and that that data is related to users in slightly different ways.
Concrete example:
I have a book-club site, where a group of users are all related to the same set of books (that their book club has read). Users can "favorite" some of those books for their own personal desire.
So, the thing I get stuck on is, where does that "isFavorite" property live in the domain model?
In the database, it's clearly in a relationship table (shooting from the hip):
* book
* user
* reading (bookID, userID, isFavorite, readAt)
... but, when I get my "entity" in my application, the part that I feel very ambivalent about is, do I combine "book" and "reading" into a *single* object:
Book:
* id
* name
* author
* isFavorite <-- From "reading"
* readAt <-- From "reading"
If I go this route, then I have to have a "userID" available whenever I get a book entity (so that it knows how to join the tables). This is OK... until you ever want to get *just* the book data, outside the context of any particular user.
So then, I think, maybe I have two entities, "Book" and "MyBook", where the latter (MyBook) is the encapsulated relationship of the various tables.
And this all makes my head hurt. Do you have any suggestions on this kind of a situation?
Hey Ben,
To answer your request in the original article, I think you'll enjoy this: http://martinfowler.com/eaaDev/PresentationModel.html. As someone else mentioned, once it gets complex enough your view should have a domain model of its own, as it were -- that is, the classic ViewModel.
To your last question in the comments, I have some thoughts that might be helpful. First thing: designing the database first is likely to lead to poor object thinking. A database is an implementation detail, an artifact of our particular way of doing computing, whereas the domain model should reflect our natural way of thinking. The domain model, and the process of modelling a domain, could, and often would, exist even if computers did not. The focus should be entirely on objects and their behaviors and responsibilities.
You can see how the data-centric mode of thinking creeps into your object model, where you think about the book first as a list of properties (including the very un-domain-like "id") rather than as a set of responsibilities.
One of the great old-school techniques for object thinking, which I noticed you naturally do in your code comments, is to anthropomorphize the object, and use the "I am a..." trick to list its responsibilities.
I am a book...
* I know my own title
* I know who wrote me
* But... I know when I was read? Hmm, that's odd. You generally don't think of books knowing that. And does the book remember all the different people who read it? Is that a book's responsibility? Or are you imagining that each person has his own book and the book just needs to remember one person's reading date? But what if 2 people share a book? Or what about an ebook? The concept of multiple copies itself gets fuzzy there... This isn't looking good.
* And all the above applies to a book knowing if it's a favorite as well.
Let's try a different tack:
I am a reader of books (user)...
* I know my name
* I know which books I've read
* I know which books are my favorites
That feels more natural. But let's try to break it down further, delegate some responsibility. Let's let real-life analogy continue to guide us. I read a lot, I have a terrible memory. Are you kidding? I can't remember all the books I've read. No problem, I keep a log in my journal....
I am ReadingJournal...
* I know all of my entries
* I know the reader who owns me
And I am a JournalEntry...
* I know my date
* I know my book
* I know if my book was a favorite
So now our Reader (user) can still have all his listed responsibilities. But except for knowing his own name, he can delegate everything else to his reading journal. And this is, in fact, quite realistic for a voracious yet forgetful reader.
@Jonah,
Thanks for the link - I'll take a look. Fowler is definitely someone to pay attention to. And, no doubt, I think about the database too early in my planning. Old habits die hard.
But, I think another issue that I have is that I build a lot of prototypes before I really start to think about the code at all. In a way, I think the UI, is parallel to the "database" is that they are on either side of the spectrum.
The UI thinks only about what the user will see.
The database thinks only about how the data will be persisted in a normalized way.
So, when I look at a user interface, and I see a user's detail page, and they have a list of books, where some of them have gold-stars, indicating "favorite", it's definitely similar to thinking about the database because now I have to think about how to gather the data to build that UI.
So, if the user can see a list of his/her books, I start to think of some RESTful API call, like:
/users/:ID/books
Now, this makes no claims about how the data will be stored; but, it is definitely tied to how I think about it in the UI.
But, looking at your suggestion of reading journal and the subsequent journal entries, I wonder if really what I *mean* is that I want the list of their journal entries:
/users/:ID/reading-journal
... which would return the books AND reading data combined.
For years, I've been building apps that query the database, then take the record set and render a view for the user. So, the idea of returning "structured data", that is not simply a serialized query, is very new to me. Definitely a mental block there.
@Ben,
But, I think another issue that I have is that I build a lot of prototypes before I really start to think about the code at all. In a way, I think the UI, is parallel to the "database" is that they are on either side of the spectrum.
The UI thinks only about what the user will see.
The database thinks only about how the data will be persisted in a normalized way.
I think this is a key. I think a decent number of developers have heard the wisdom that you shouldn't begin with the database. But far fewer have heard the wisdom that you shouldn't begin by making the UI. In fact, most believe this is the only correct place to start. It was a revelation to me when I first saw this truism questioned. The following is from David West's "Object Thinking":
A worse error was propogated when many of the early tutorials on object programming introduced a misconception by suggesting a "method" colloquially referred to as "cocktail napkin design." It was suggested that the correct way to design an application was from the interface in; that is, sketch your interfce on a cocktail napkin and then find the objects necessary to implement that interface. The GUI became a straightjacket to which objects had to conform. This, in effect, meant that object design and implementation were little more than the hard-coded reflection of the specific and idiosyncratic design of the a set of visual interfaces. Change the the visual interace, and you had to change the object. Not only did this make for a lot more work, it meant that objects were not reusable in different contexts if those contexts defined visual interfaces in an alternative fashion.
Note
"You can't emphasize this point enough," suggests Ken Auer, speaking about the danger of "GUI in" design. "In my early days of OO, if you talked to someone who had been using Smalltalk for 1 to 3 years, you could almost rely on the fact that they 'got it'. After the advent of Parts, VisualAge, and (to a slightly lesser extent) VisualWorks, I had many interviews with programmers who had been 'programming with Smalltalk' for 2 or more years and didn't realize there were supposed to be some objects other than the GUI and the database. Even the ones that recognized this tended to have a poor handle on how central the domain objects shoudl be because they probably spent a good two-thirds or more of their time dealing with GUI and/or DB issues. Ken's comments support a basic premise of this book: object thinking is most easily corrupted by reverting to old, familiar forms of thought. Laying out widgets on a form and objects as data entities are but two examples.
@Jonah,
I am definitely in the camp that believes that the UI *should* come first, before any coding is done. I think the UI informs the engineering team what functionality is even needed at all (and which is not).
That said, the original basis of this blog post was, I believe, in heavy alignment with the fact that the UI should *not* be tied to the domain model. That the UI is simply a "report" on the state of the application and may bypass the domain model altogether.
The complexity this raises, however, is that I need to then have two understandings - what is the domain model? And, what is the report model? And, how are those related?
So, for example, let's say I have an API:
/users/:ID/reading-journal
... that gets the list of reading entries. And this list has a toggle button on each rendered record that sets the favorite flag to true/false. I might have an endpoint like:
/users/:ID/reading-journal/:ID/mark-as-favorite
... now, say that this RESTful controller applies the request and then wants to return the updated data in the response. Is the data that gets returns the domain-model? Or, is it an update in the "report-oriented data"?
If the former, it is much more flexible as a general UI. If the latter, then even the interactions are very strongly coupled to a particular UI.
... anyway, more to think about.
@Ben,
Good conversation.
I am definitely in the camp that believes that the UI *should* come first, before any coding is done. I think the UI informs the engineering team what functionality is even needed at all (and which is not).
Ah, yes. This is not in contradiction with the passage I posted. Whether or not to prototype or even completely build a UI before coding is an orthogonal issue, and I agree with you on this point (and I'd imagine David West does too, but I can't recall if he discusses this specifically). Coming up with your domain model does not imply you will be coding. This step could be done on CRC cards, with object cubes, and for some highly experienced coders in their heads. The point is that you should understand your domain and your domain objects as the first step. It will inform you understanding of the many kinds of UI that might come up, and will give you perspective that will inform the specific UI you end up prototyping. UI, code, database -- all these things are volatile. The basic domain objects, if properly modeled, should be the most stable and flexible part of your system (which is not to say completely static).
I don't have time to address your other comments properly today, so I will try to post again tomorrow.
Jonah
Well, still awake, so here goes with the rest of my answer :)
That said, the original basis of this blog post was, I believe, in heavy alignment with the fact that the UI should *not* be tied to the domain model. That the UI is simply a "report" on the state of the application and may bypass the domain model altogether.
Well, I think what your example demonstrates well is that the UI is not a 1-1 projection of either the database objects or the domain model objects. The view still depends on the model, both in classic MVC and web MVC, and almost by necessity. Even in MVVM, where the view depends on the view model, the view model is just a kind of mediator between the view and the model. And even in web MVC, where the convention is typically to translate the model objects into simple primitives or arrays or basic key value stores before passing them onto the view, you still don't really get around the issue. Saying it's a report on the state of the application (which I think is a useful way to think of it) is really just saying that the view usually depends on a number of different model objects at the same time.
The complexity this raises, however, is that I need to then have two understandings - what is the domain model? And, what is the report model? And, how are those related?
There is no complexity here that isn't fundamental to the UI. There is nothing "extra," so to speak. You domain model is still your domain model, and has whatever complexity it has. Your UI can be as simple or complex as you want it to be. In either case, you'll need to model it. Now the view uses the behavior exposed by your view model (think angular controller methods, eg) and the view model, in turn, delegates to the methods of the domain objects. And the interface for those domain objects will often be an API endpoint.
Now, if you make some actual meaningful UI and then compare it to say a default admin CRUD interface for directly editing your database tables, then sure, it's going to seem complex. But that's only because in the latter case you get your view model for free since you're essentially calling domain model methods directly. Your view model just happens to be the same as your domain model.
So, for example, let's say I have an API:
/users/:ID/reading-journal
... that gets the list of reading entries. And this list has a toggle button on each rendered record that sets the favorite flag to true/false. I might have an endpoint like:
/users/:ID/reading-journal/:ID/mark-as-favorite
In this case, the API endpoint is essentially an interface to your existing domain object, ie, "JournalEntry.favorite()".
... now, say that this RESTful controller applies the request and then wants to return the updated data in the response. Is the data that gets returns the domain-model? Or, is it an update in the "report-oriented data"?
If it's just plain data, it's not a domain object. But that's just a nitpick. Nothing is different between this request and the original request "/users/:ID/reading-journal". The data that gets returned is just a response from a domain object method. The question is a little odd here since it doesn't make much sense to return "data" in this example: it would make more sense to return a success or error message. So I guess... maybe I don't understand your confusion, or maybe I don't understand the question.
@Jonah,
First off, I truly appreciate the responses. I am historically a "procedural" programmer, so the transition (aka, multi-year journey) into something that is more object-oriented has been a long and frustrating one, to say the least.
Everything that I say comes from the shores of SQL-island and looks outward :) For example, when I say that the UI data is a "report", what I really mean is that it bypasses the core domain model and goes almost directly to the persistence layer:
UI --> Reporter --> SQL
... where as a "command," to change the state of the application, would go through the core domain model:
Command --> Use Case --> Domain Model --> ?Repository? --> SQL
Essentially, the "UI reports" understand the domain model, but only in the sense that it is represented by the database relationships, not by its [the domain model] classes.
In my limited experience, both the UI reports and the domain model are pulled from the same database; but, I suppose the reporting database could be a completely separate thing - like a document database or different set of tables that store aggregate data.
The question is a little odd here since it doesn't make much sense to return "data" in this example: it would make more sense to return a success or error message. So I guess... maybe I don't understand your confusion, or maybe I don't understand the question.
I think I have an extra layer in my architecture - so the controllers don't actually talk to the domain model directly, they talk to some sort of use case, workflow, or service object (not sure what the right terminology would be).
Pseudo code might look like this in the Controller:
... so, the "application core" wouldn't return the updated data - as you say, it would just return a boolean; however, and this may be specific to our application approach, we tend to have our web-controller layer echo back the updated information to help with the UI rendering.
In my current app, we have a lot of client-side caching, so this approach helps us keep that cache up-to-date. On the client-side, our service layer that makes the actual HTTP AJAX requests can make requests, and then cache the most up-to-date response.
That said, perhaps this latter approach does confuse things because I am a request from a *specific* UI to a *general* API and returning *general* data. Perhaps a better approach would be to return non-data (ie. True) from the *general* API, and then have the client-side code go back to its *specific* reporter for more data (if it feels the need to).
I think we were trying to make our API interactions less chatty.
I think I need to play around with some code. So much to keep in my head.
@Ben,
First off, I truly appreciate the responses. I am historically a "procedural" programmer, so the transition (aka, multi-year journey) into something that is more object-oriented has been a long and frustrating one, to say the least.
My pleasure, I feel like I'm just giving a little back for all the angular help your articles have given me. And I feel your frustration. I don't want to paint myself as the ultimate master OO guru, but I've been spending a lot of time the last year going back to the original literature so I could truly "get it." The problem is that much of the current literature, as well as blog posts (even stuff written by some really smart, accomplshed people) still misses the real spirit of OO imo. It sometimes seems to me like this lost art that reached it's apex in the 70s and 80s, and has in many respects regressed since then.
Command --> Use Case --> Domain Model --> ?Repository? --> SQL
Essentially, the "UI reports" understand the domain model, but only in the sense that it is represented by the database relationships, not by its [the domain model] classes.
So this last part, I think, may indeed be problematic, since your UI reports (view models) are depending directly on your database implementation. What happens when you switch from MySQL to Mongo, or just decide to restructure your db for whatever reason, etc? Now you've broken your view code. The central shift in perspective that needs to be made is that the database is itself just a kind of "view" of your domain model (just a machine-friendly, rather than a human friendly, one). So really you have one view depending on another, which is not good. Quoting again from David West's book:
It's easier to illustrate ideas about an object having multiple appearances by using visual metaphors. But visual representations are not the only appearances an object might have. Imagine an object that needs to store itself in a relational database. The relational database cannot accept the object in its full natural glory, so the object must marshal itself into a stream of bits that can be accepted and held by the RDBMS. The resultant stream of bits constitutes an appearance of the object but is not the object itself, any more than a visual representation is.
And with a normalized database, this "hard disk view" of a single object may be distributed across multiple tables. Typically the domain object will delegate the details of this storage procedure to an ORM object. And this is the source of lots of confusion, because people mix up the ORM object and the domain model. In many cases they are the same object, and the two terms are applied interchangeably. Most of the popular web MVC frameworks, including Rails, encourage this confusion, and most developers consider their domain model to be their ORM objects. In simple applications this is not such a problem: the approximation is good enough. But in general this need not, and should not, be the case. Your database is *not* your domain model. Better to think of it a serialization mechanism for your domain model, ie, a machine's "view" of it. And when you think about your domain, you should not concern yourself with your database's details, any more than you concern yourself with physical memory sectors on your hard drive when you think about how to organize your files and directories.
I like to think of the paradigm shift needed here as a sort of rebellion. We've been told all these years that we need to think in the database's terms. We've learned about the 3rd normal form, and learned how to create and read database diagrams, to the point where it's pretty easy to do so now, and we're all very proud. But no! This is like a slave being proud of how good he is at pleasing his master. You need to recapture your confusion from the early days, when slicing up your data cow into all its component organs and laying them out side by side on a table seemed like such a strange view of a cow -- indeed, not like a cow at all. And that's because it's not a cow! So rise up to the database! Insist that his cow is not the real one. Yours is!
I think I have an extra layer in my architecture - so the controllers don't actually talk to the domain model directly, they talk to some sort of use case, workflow, or service object (not sure what the right terminology would be).
Pseudo code might look like this in the Controller:
function markAsFavorite( bookID ) {
. . // Returns true or void or throws exception.
. . bookService.markAsFavorite( session.userID, bookID );
. . // Returns updated book record to client.
. . return( bookService.getBook( session.userID, bookID ) );
}
It's hard to say definitively without knowing the details of your app, but in the above code "bookService" looks like it should be a domain object. It's hard to comment on if it's a well designed one, or if you're just using an ORM object, or something else. But to me it doesn't feel that natural. You have the user id from the session, which means have a handle to your User domain object. So "user.markAsFavorite(bookId)" seems more natural to me. And if you wanted to keep things purer so that User need not concern itself with the creation of book objects, you could do something like:
book = new Book(bookId) // book domain object. Will delegate to book ORM to create itself. For simple cases could be the same object, but the conceptual distinction should still be clear to you
user.markAsFavorite(book) // user domain object, already constructed somewhere based off session id.
Jonah
@Jonah - You should be writing blog posts about Object Oriented Programming. Thank you for your insight and contribution to this thread.
@Jonah,
If there's any books you'd recommend on the subject of domain modelling, I'd love to hear it. I just downloaded the free PDF of "Domain Driven Design Quickly". Figured I'd give it a quick read before tackling Eric Evan's book.
What happens when you switch from MySQL to Mongo, or just decide to restructure your db for whatever reason, etc? Now you've broken your view code.
For me, I don't see this as being a huge deal. Yes, it will break a lot of view-oriented stuff; but that's because new optimizations are required. In fact, switching from a relational DB to a document DB would be a significant change in view-data collection. Instead of creating SQL queries that perform optimized JOINs, maybe I have a single "document" that caches what that JOIN would have created.
I don't know very much about NoSQL databases; but, I know they offer tradeoffs that would need to be considered.
That said, this would be for view-oriented data only. If we were talking about the core domain-model, hopefully that would be encapsulated behind some persistence mechanism whether it be ORM or some sort of "repository" or "gateway" pattern.
NOTE: Again, I come mostly from the SQL view-point; so when I say things like "repository", understand that I say that theoretically.
Regarding the extra layer I have, more what I was trying to say is that I have a layer that exposes "simple" data to the outside world, such that the controller posts simple data (ie. strings, numbers, arrays, hash maps) to the "application layer".
This application layer then converts that simple data into domain entities, does work, and then returns the results as simple data.
Essentially, the application layer would completely encapsulate the inner workings and implementation of the app. Maybe its uses a rich domain model - maybe it uses transaction scripts - the controller doesn't know that; the controller just knows "Data-in, data-out."
When it comes to the actual domain model and whether a behavior should be on an entity; or if it should be on a service (that coordinates entities), I simply don't have that much experience.
@Josh,
Thanks!
@Ben,
I definitely recommend the David West book "Object Thinking" I've been quoting from. It goes deeply into the philosophy and history of OO programming. His breadth of knowledge is impressive. It's a strange book though, not your typical hands on how-to book. I think this one is a love it or hate it book, and I loved it.
http://www.amazon.com/Streamlined-Object-Modeling-Patterns-Implementation/dp/0130668397
This one is excellent too. This is much more hands on. While Peter Coad is not one of the authors, this book is kind of a distillation and enhancement of his previous books. It lays out all the recurring patterns of object relationships. Not exactly patterns in the Gang of Four sense, but at even more general level. Gives you building blocks for solid OO modelling.
Next up Martin Fowler's:
http://www.amazon.com/Patterns-Enterprise-Application-Architecture-Martin/dp/0321127420/ref=sr_1_1?s=books&ie=UTF8&qid=1368648617&sr=1-1&keywords=martin+fowler
And finally I'd highly recommend the blog of Carlo Pescio. Start with his two most popular posts:
http://www.carlopescio.com/2011/04/your-coding-conventions-are-hurting-you.html
http://www.carlopescio.com/2012/03/life-without-controller-case-1.html
If you get to any of these, please post back here and let me know what you think!
Jonah
@Jonah,
Thanks for the book recommendations. I am looking them up right now. I can see that Object Thinking is available for the Kindle App - sweet! Also, I just recently heard Martin Fowler on the Ruby Rogues podcast, talking about POEAA:
http://rubyrogues.com/097-rr-book-club-patterns-of-enterprise-architecture-with-martin-fowler/
Seems like everyone loves it.
Thanks so much for all the recommendations. I'll really try to get some reading done. I also just signed up for my local DDD (Domain Driven Design) Meetup group here in NYC :)
@Ben,
No problem. I'm curious to see what you'll think.
By the way, I've been delving into angular more and have like half an answer so far to the interesting question you posed here: www.bennadel.com/blog/2447-Exploring-Directive-Controllers-Compiling-Linking-And-Priority-In-AngularJS.htm
I'm finishing up a project and was going to delve into the angular source more before posting anything, to see if I could understand it 100%. Or if you've since found an answer, please post in the comments as I'd like to know.
Jonah
@Jonah,
I've been reading "Object Thinking" for the past few days. So far, definitely an interesting book. He goes into a lot of history and philosophy, which can get a little frustrating (which he freely admits in the book itself); but, I am trying to be patient :) I definitely do want to think better about this stuff, so I am trying hard not to rush through the book!
@Ben,
Yes, that's why I think it's a love it or hate it kind of book. It can feel dense and meandering at times, but I think the price is worth it for his insight. The way I see it is that he has the bird's eye view of the history of OO programming in his head -- its initial motivations, its birth pains, its evolution and all the side tracks along the way. And to understand it you need to understand some of the philosophy behind it. It's not just a programming paradigm, it's a new way of looking at the world.
I think that's his goal: to give you that completely new perspective.
In fairness, it could probably be done more efficiently than he does it, but I haven't found much else that even makes the attempt, except Carlo's blog to some extent. I'm sure they do exist though.
@Ben,
Oh also, here's a talk he gave that I enjoyed:
http://www.infoq.com/presentations/transcendence-gate-dave-west
@Jonah,
Interesting presentation. I'm currently about 40% through the book (Kindle doesn't show you pages, it shows you some odd "location" data for your book). This book has like 7,000 locations. Very odd.
I'm struggling a bit with the book. I've definitely started to skim parts of it, trying hard to slow down for areas that are a bit more pragmatic.
One of the things I am having a hard time coming to terms with is all the event-based communication. In a JavaScript world, I love event-based systems. I'm not saying that I use them exactly the way that he does; but I use a lot of events in JavaScript.
In my server-side code, however, I use very little event-driven development. But, part of the reason for that is that so few objects actually exist at any one time. As such, it's not like I can attach an event to a "Product" object because that product object is about to be persisted and then removed from memory.
It seems the best I can hope for is that the object that "coordinates" with product (which is likely some sort of singleton and will remain in memory) can announce events when a product does something. But, my problem with this approach is that I see no significant different between that and the "coordination" object just telling other objects to do something when a product does something.
After all, the various objects still need to know to register a listener with some coordination object, which means that the developer still needs to remember to "make" that relationship.
Of course, if I used a single event-queue, like I do in JavaScript sometimes - "ModelEvents" - then no relationship to the various objects would need to be made, only relationships to the event queue.
Argg, need more clarity :D
Anyway, still making my way through the book. I will finish it! It's very rare that I don't at least finish a book (even if I read it quicker than I would normally).
@Jonah,
Over the weekend, I finished the Object Thinking book. Not sure how much I am actually able to take away from it. It had some provocative passages; but, mostly I have more questions than answers.
If you're curious:
www.bennadel.com/blog/2483-Object-Thinking-By-David-West.htm
I was looking at the Streamlines Object Modeling Patterns book on Amazon. I might try to give that one a shot next.
I was also finding Carlo Pescio's blog very interesting too! Seeing him walk through the modeling of the Mine Pump example was super fascinating.
@Ben,
Regarding the product question, could you give more details about the problem you're solving and the current solution. I'll see if I can think of any object thinking solutions that might apply on the server. Currently traveling but will be home in 2 days.
@Jonah,
All I mean is that I don't know how much event-driven programming works IF you don't keep all your objects in memory at the same time.
For example, let's say I have Subscription objects that have some expiration date. It wouldn't be feasible to, say, bind to the "expired" event on Subscription, because they are not stored in memory over time.
What seems feasible, to me, is to have some sort of Gateway/Repository that can query the persistence for "subscriptions that should expire." Then, once that collection is in memory, explicitly tell them to expire and explicitly do all the other stuff that would need to be done (such as sending out email to the user).
What seems feasible, to me, is to have some sort of Gateway/Repository that can query the persistence for "subscriptions that should expire." Then, once that collection is in memory, explicitly tell them to expire and explicitly do all the other stuff that would need to be done (such as sending out email to the user).
Great question. The best way to implement an OO solution (at least in spirit) will depend on the specifics of your situation: for example, you might have an ORM which can automatically build and load into memory the necessary collobarating objects that need to be notified.
But let's assume that's not the case, or that it would be too complex. I think now your point stands, but we can still look into the deeper design objectives we're trying to achieve with an event-driven approach, and see if we can still achieve them.
Can we perhaps mimic the "eventDispatcher" West describes in your situation? To make the discussion concrete, let's say you have a cron job which queries your database every hour checking for expired subscriptions. When they are found, an email must be sent, and perhaps a number of other things. Our real concern is that these "other things" may change, or that next week there may be more of them. So the thing we want to avoid is having some big method somewhere (in the cron script, or in the script called by the cron script) that's responsible for doing all the stuff we do when a subscription expires.
And there are lots of ways we can avoid this. For example, we can create a folder called "onExpired" which has a bunch of scripts (php, ruby, coldfusion, whatever), and these scripts make a single assumption: when they're called, they'll be passed a subscription id, or perhaps an Subscription object (conceptually, you can think of it as an object in both cases). They can use that id or object to get whatever other info they need from the database, directly or indirectly via ORM or model objects, and then do their work (send an email, whatever). The script itself could do nothing more than create some other object where the logic more appropriately belongs (like an "EmailNotification") and invoke a method on it.
So your cron job queries the database, and then calls each script in the "onExpired" folder, passing along an object or id for the script to work with. Again, this specific solution isn't important or necessarily good -- the point is that we can still mimic the object design we want.
The important thing is to see that the problem you're facing is just an implementation detail arising from the need to use of a database. It should have little effect on our conceptual model, or the goal of decoupling "expirations" and "stuff which happens on expiration." It just requires us to do some extra implmentation work, rather than having language facilities automatically take care of everything for us.
@Jonah,
As I was reading what you wrote, it occurred to me that maybe I do something similar to that in some of my client-side code. In an application I'm working on, there are a bunch of unrelated interfaces that may or may not be rendered at a given time (ok, they're not entirely unrelated, but they don't communicate too much).
Anyway, since several UIs might have to react to data that they don't know is loaded, rather than listening to a given object, they all listen to a centralized event-dispatcher: modelEvents.
"modelEvents" is just a pub/sub mechanism that various controllers, caches, and other service objects subscribe to. Such as:
modelEvents.on( "projectCreated", callback );
... then, the service layer that handles the "project-create" action will confirm the successful persistance of the data and then trigger the event:
modelEvents.trigger( "projectCreated", newProject );
... then, anyone know needs to know about that event will get their callback invoked.
So, rather than subscribing to an "Entity" that announces events, things subscribe to a central event node.
This has some nice benefits in that it allows different ways to announce an events. Sometimes the event happens on a given client; sometimes, the event happens on the server and is then pushed to various clients over WebSockets... and the WebSocket handler can then turn around and trigger events off of the modelEvents pub/sub object.
That said, I find the very concept of working with "events" much easier on the client-side than the server-side; probably from the years of working with JavaScript.
@Jonah,
I know it's been a few months, but I am *still* trying to make my way through "Streamlined Object Modeling." I got about one-third of the way through the book and it was completely mind-numbing :) All this philosophical talk about places and things and containers and events and transactions... but with no actual implementation details, which I can't follow.
So, I took a detour through MongoDB.
But, then I picked it up again over the weekend and realized that I was about to enter a section where they actually start talking about code and how the philosophies in the previous part get applied!
So, now I'm back at it. Hopefully, I'll be able to wrap my head around what they are saying. I found the first part of the book very much over my head.
@Ben,
Oh dear, I feel I am 0 for 2 with recommendations for you :(
While I agree the streamlined object modeling book can be dry and text-booky, I actually found it to be practical as well. I'd be curious to hear which parts you felt were over your head, as I am certain the underlying concepts are not. Maybe I have a higher tolerance for opaqueness in the OO literature simply by necessity -- the subject matter, I think for historical reasons, seems to invite it (sadly, because it shouldn't).
I will go ahead and push my luck and give you one more link of recommendations:
http://objectsonrails.com/#sec-23
The object on rails book is good, and points out a lot of the deficiencies in the standard practice of rails I alluded to in one of my posts above I think. The insights would apply to most web frameworks today, not just rails.
Cheers,
Jonah
I'm afraid I can't contribute much to the discussion at hand, but I have to say I do like the last name of friends used in the first example up there. :-) haha....nice. Speaking of names, interestingly, I went to school (high school and even before) with a guy named David West, but I really don't think it's the same guy. lol. He didn't really hit me as a programmer type. Maybe, but highly doubtful.
@Jonah,
Hold on, good sir! I am not hating on the book... yet :P I'm just saying that the first 1/3 was a bit over my head. But, let me explain a bit more. The first 1/3 was super exciting as far as what they were saying. For example, when they were laying down rules about (forgive my mistakes off the top of my head) "Whole - Part" relationships and they were talking about how "validation" of relationship is delegates to *both* the Whole and the Part and that certain things take more responsibility....
.... that was super exciting. I was like "Yes! Yes - this is exactly the kind of stuff I need to learn about."
The problem was, it was like 100 more rules *just* like that one, but without any practical examples. I mean, sure they talk about VideoTitles and VideoTapes, and there's diagrams; but, half of what confounds me is simply understanding at the code-level. Specifically, who creates that? How does that get persisted? How do the dependencies get created? Etc...
Now, it looks like the later half of the book might be going into that sort of detail. They seem to be building it up incrementally. Like, they have "Team - TeamMember" , but they don't talk about the "validation" rules on that until *next* chapter. So, I'm gonna keep reading, hoping that it gets there!
@Anna,
You can't go wrong with a few Annas here and there ;)
@Ben,
So, last night, I reached Chapter 8 of the Streamlined Object Modeling book and it says:
"8. Implementing Business Rules ... This chapter shows how to implement business rules in programming code. In a sense, this chapter is what the whole book has been building toward. Previous chapters showed how to choose objects, define business rules, and code objects using the collaboration patterns. This chapter shows how to enforce real-world business rules with object methods organized by the collaboration patterns. Writing code without business rules is like solving physics problems without considering air resistance. This chapter considers air resistance. Sure, it takes a little more effort, but without it, your parachute would not work."
... so this is exciting. This is exactly the kind of information that I am looking for; and, I hope that once I have a more concrete understanding, I can go back and put the rest of the book in context.
@Jonah, that last message was supposed to be @YOU - still waking up :)
@Ben, I agree...thanks! And I was thinking you were talking to yourself there, so thanks for explaining yourself. haha
@Jonah,
I'm really starting to get into the Streamlined Object Modeling book. Chapter 8 (and I'm about to start Chapter 9) are very fascinating. I think this is really the kind of stuff that I need to start to wrap my head around. It's so different from how I approach problems now (with my "transaction script" mentality).
To try and work through some of these ideas, I decided to create a project on GitHub where I could flesh out a JavaScript domain model and apply some business rules around properties, collaborations, coordinations, etc.
https://github.com/bennadel/Streamlined-Object-Modeling
Right now, it's just a ReadMe file; but, as I start working on it, I would be honored if you would stop by occasionally to help me out!
@Ben,
I'm honored that you're honored :)
I'd love to help out. I'm sure I'll learn something new and will be good to brush up on the book.
I just watched the repo on github, and I have to say I love the example. Looking forward to this!
@Jonah,
Awesome sauce! This is so exciting!
@Jonah,
I've decided to go with RequireJS to load the modules for the exploration since I think it will help me keep them all logically AND mentally separate. As of this moment, I basically just tried to get RequireJS to work (which took some time since I haven't touched it in a while); but, it is currently loading several empty classes.
Now it's time to actually start thinking about the domain model :D I'd like to really try to follow the book in its separation of concerns and the "DIAPER" approach.
There's gonna be a ton of flipping between the code and the book, book and the code, and so on and so forth.