Populating An Existing, Formatted Excel Document Using ColdFusion And POI
Last week, I was tackling the problem of providing a simple way to format Excel documents using ColdFusion and POI. In the comments to that post, Alan Johnson suggested that instead of trying to create a completely new Excel workbook, that I use an existing Excel workbook with pre-formatted cells. This was absolutely genius. Genius I tell you! I can't believe I never even thought of this.
This kind of solution would be great for reporting systems where you want to create highly customized reports that need to get run on a regular basis. Something repeatable, something whose data is dynamic but whose layout is not. To test this idea, I created a "blank" Excel document and formatted the cells/columns/rows that way I wanted them to end up in the final report:
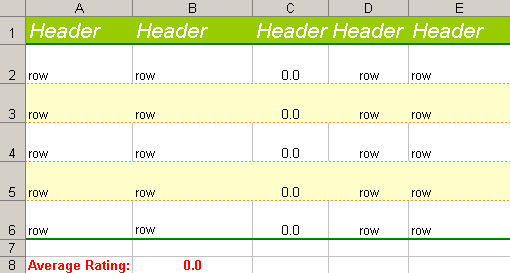
As you can see, the header and data cells are already formatted complete with background colors, borders, text formatting, text alignment, text wrapping, and there's even a formula that averages the song ratings. Now, it's just a matter of populating them:
<!---
Create an array to hold data that we are going to use to
populate the existing Excel sheet. This array will be an
array of arrays representing rows of columsn.
--->
<cfset arrData = ArrayNew( 1 ) />
<!---
Populate the data array. To do this, we will just convert
several lists to arrays. Each of these lists will represent
the columns within a given row.
--->
<cfset arrData[ 1 ] = ListToArray(
"Artist,Song,Rating,Length,Play List"
) />
<cfset arrData[ 2 ] = ListToArray(
"Over The Rhine,All I Ever Get For Christmas Is Blue,9.5,4:25,Blue Night"
) />
<cfset arrData[ 3 ] = ListToArray(
"Over The Rhine,Darlin' (Christmas Is Coming),8.0,3:35,Easy Afternoon"
) />
<cfset arrData[ 4 ] = ListToArray(
"Nina Simone,In The Dark,9.0,2:15,Makeout Deluxe"
) />
<cfset arrData[ 5 ] = ListToArray(
"Norah Jones,Turn Me On,9.0,2:33,Makeout Deluxe"
) />
<cfset arrData[ 6 ] = ListToArray(
"Peter Gabriel,In Your Eyes,10.0,5:29,Break Up"
) />
<!---
Now that our data arary is populated we can go about
creating the Excel workbook. When we create this Workbook,
we are going to read in an existing Excel sheet that
already has set formatting. Read in the Excel file using
a File Input Stream.
--->
<cfset objWorkBook = CreateObject(
"java",
"org.apache.poi.hssf.usermodel.HSSFWorkbook"
).Init(
<!--- Create the file input stream. --->
CreateObject(
"java",
"java.io.FileInputStream"
).Init(
<!--- Create the file object. --->
CreateObject(
"java",
"java.io.File"
).Init(
ExpandPath( "./pre_formatted.xls" )
)
)
) />
<!---
Now that we have read the existing Excel file into the
WorkBook, let's get the first sheet. This is the sheet
to which we will be writing data, but mainting the
current format.
--->
<cfset objSheet = objWorkBook.GetSheetAt(
JavaCast( "int", 0 )
) />
<!---
Loop over the rows in the data array to start populating
the Excel file with data.
--->
<cfloop
index="intRow"
from="1"
to="#ArrayLen( arrData )#"
step="1">
<!---
Get a pointer to the current row. This will make
referencing it easier as we make are way through
the data. Remember that our ColdFusion array is
one-based, but the rows index is Java and
zero-based.
--->
<cfset objRow = objSheet.GetRow(
JavaCast( "int", (intRow - 1) )
) />
<!---
Loop through the "column" values in our data array
(for this row index).
--->
<cfloop
index="intColumn"
from="1"
to="#ArrayLen( arrData[ intRow ] )#"
step="1">
<!---
Get the cell object whose value we want to set.
Remember that while ColdFusion is one-based,
the index of the cell is zero-based.
--->
<cfset objCell = objRow.GetCell(
JavaCast( "int", (intColumn - 1) )
) />
<!---
For this example, we know that one of the columns
is numeric. We could have just set the value based
on the column index, but I have chosen to go with
a simple numeric check.
--->
<cfif IsNumeric( arrData[ intRow ][ intColumn ] )>
<!---
Set the numeric value. We are setting it as a
float, but the API and the existing Excel
formatting will take care of the display.
--->
<cfset objCell.SetCellValue(
JavaCast(
"float",
arrData[ intRow ][ intColumn ]
)
) />
<cfelse>
<!--- Set the string value. --->
<cfset objCell.SetCellValue(
JavaCast(
"string",
arrData[ intRow ][ intColumn ]
)
) />
</cfif>
</cfloop>
</cfloop>
<!---
Now that we have populated our existing Excel file with
data, let's write the updated Excel data to a new data
file. We do NOT want to overwrite the pre-formatted file
as we want to be able to use that again to created
pre-formatted Excel sheets.
--->
<cfset objWorkBook.Write(
<!--- Create the output stream. --->
CreateObject(
"java",
"java.io.FileOutputStream"
).Init(
<!--- Create the file object. --->
CreateObject(
"java",
"java.io.File"
).Init(
ExpandPath( "./pre_formatted_data.xls" )
)
)
) />
Doing this produces this new Excel document:
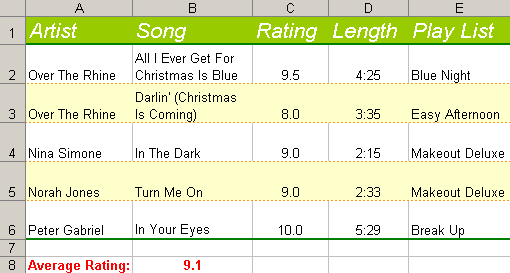
Notice that all the formatting was kept exactly as it was in the original document. Also, if you look at the code, notice that the outputted document is a different physical file that than the pre-formatted, input document. This allows us to keep a standard format document and then repeatedly generate new documents.
This is very cool! I can already see where this would come into use. I'm thinking corporate logos, freeze panes. I know that this sort of stuff can be done using the POI interface... but why do it if you don't have to? Of course, I still want to come up with a way to easily format Excel documents using some sort of API, but this solution is pretty badass.
Thanks Alan Johnson!
Want to use code from this post? Check out the license.

Reader Comments
I'm blushing Ben. Thanks.
I'm just glad it all worked ;*) .... Cheers!
Hi Ben
I think the most powerful use of using an existing xls as a template is that you get to include charts. There's no way to use the poi stuff to create a chart, but you are supposed to be able to load data into the right places so that existing charts display with your dynamic series data.
Antony
Antony,
Yeah, that is some seriously cool stuff. Charts and graphics. It's very cool!
Ben, thanks for all your work on the POI interface. I have found another Java package that takes the idea of populating an existing, formatted Excel Template. It is called jXLS and seems to work pretty well. It uses the Jakarta POI package. It is a separate java class install (i.e., copy a file to a CF server directory), but is also free.
I have written 2 blog posts about jXLS. The first is just what and why and references your work: http://mattw.mxdj.com/populating_an_existing_formatted_excel_document_using_coldfu.htm
The second is how to install and some sample usage code.
http://mattw.mxdj.com/using_jxls_and_jxlsutiltiycfc_to_export_excel_files.htm
Although it seems to solve a different need than what you have been working on, some of your readers may find it interesting.
This looks pretty cool, but I have a question for you, I am in need of something liek this, however, in my template, I need to create a dynamic amount of formatted items...
Is there a way to create extra formatted rows?
@David,
Try looking at this:
www.bennadel.com/index.cfm?dax=blog:484.view
It talks about using the POI Utility to apply basic CSS to the query record set. It is not perfect but it is the best I have to offer just yet. But, don't download that version of the POI, use this one, it is the most up to date:
bennadel.com/index.cfm?dax=blog:624.view
I need to add a row to the spreadsheet every time some data is submitted. I want to put it at the next available row, but how do I know where that is?
It doesn't seem that Ben has included it yet, but the java method to get the last row number is
getLastRowNum()
Hope that helps.
That's great that I found this POI useful to populate values into existing formatted excel report.
However, if the worksheet has an image and I tried to run the script you wrote, the image disappeared together with the formatting. I want the image to remain there.
Excel error occurred:
------------------------------------------------------------------------
Microsoft Office Excel File Repair Log
Errors were detected in file '\\server2\website\_poi\poi\pre_formatted_data.xls'
The following is a list of repairs:
Damage to the file was so extensive that repairs were not possible. Excel attempted to recover your formulas and values, but some data may have been lost or corrupted.
I could not figure out why Microsoft Office Excel File Repair Log
------------------------------------------------------------------------
@Eileen,
I have not worked with images in Excel and POI yet. I will post anything that I find.
@Eileen,
We also found this to be the case with CF7... however, for some reason it would still work in CF6. Not all images, but it could still handle most of them.
I haven't found any workaround for this in the later versions of Cold Fusion.
alan
FYI... Also we've noticed that the best xls format to work with POI is Excel version 97-2003/2005
This is awesome man thanks. Current project was giving me a huge headache and this is exactly the solution I needed.
Thanks a million!
@Ryan,
Glad to help out. Make sure you check out the most updated project for POI. It has some cool tag-based output:
www.bennadel.com/projects/poi-utility.htm
I get an 'Object Instantiation Exception' when try to load my current excel file. It works fine with a simple excel file but my file contains macros or something else that this seems to have a problem with. I get the error on
'ExpandPath( "./new_report_template.xls" )'.
The stack trace indicates
'Caused by: org.apache.poi.hssf.record.RecordFormatException: Unable to construct record instance, the following exception occured: null'.
Any ideas for a non-java programmer?
@Bret,
Sorry, no suggestions from me. I have only dealt with less complicated documents.
@Bret
What version of Excel is your template saved as? Try to keep it Excel 97-2005 version, since we've found that is the most agreeable to be used with POI.
Alan - After reading one of your earlier posts I saved the file as Excel 97 - 2003 & 5.0/95 Workbook. It doesn't appear to help my situation. Thanks though.
If you have images in the excel doc, you might want to start by stripping those out first. Macros are usually okay to have in the file. Images (since CF7 and above) seem to cause issues.
I'm using CF8 dev edition and when I use the example code I get an error saying the variable objcell is undefined. It definitely is defined. I think it has something to do with the javacast(). I'm not sure. Can anybody help? pls. thx.
Great info Ben. But I got a problem. In your sample you build a data array of data for your input. I need to use a db query. I'm not quite sure how to do that but I found some other code to create an array from my query. But I'm getting an error: Variable OBJCELL is undefined.
This is my code:
<cfquery dbtype="query" name="makexcel">
Select site_id,request_type,part_number,part_desc,detail_number,receipt_date,Ship_date,ship_via,waybill from getpr
</cfquery>
<!--- Populate the array row by row --->
<cfloop query="makexcel">
<cfset arrData[CurrentRow][1]=site_id>
<cfset arrData[CurrentRow][2]=request_type>
<cfset arrData[CurrentRow][3]=part_number>
<cfset arrData[CurrentRow][4]=part_desc>
<cfset arrData[CurrentRow][5]=detail_number>
<cfset arrData[CurrentRow][6]=receipt_date>
<cfset arrData[CurrentRow][7]=ship_date>
<cfset arrData[CurrentRow][8]=ship_via>
<cfset arrData[CurrentRow][9]=waybill>
</cfloop>
The rest of the code is from your example. Any ideal what I'm doing wrong? Thanks, Jim
@Jim,
You might find it easier to use the POI Tags that I have added to the latest versions of this project:
www.bennadel.com/projects/poi-utility.htm
It allows you to use an Excel template (see sample files in download).
I am just about to release an optimized version that is much faster.
Ben,
You just rock!!
I discovered your POI cfc a couple of weeks ago when i had to read a multi-sheet xls file and it saved my life! (or maybe just my sanity!).
now I have another client who wants a "pretty" excel sheet to download and print and here you (and Alan) are with the solution again.
What a relief not to be hacking away with the old rudimentary csv and excel solutions any more!
thank-you, thank-you, thank-you!
@Rochelle,
Glad you like. Be sure to check out the POI project which has a bunch of demos:
www.bennadel.com/projects/poi-utility.htm
@Eileen,
Hi Eileen - did you ever resolve this issue, as I'm getting the same results at the moment?
The rest of my POI code is working fine and if I use the branded template that Ben supplied, I see my content below his logo, but with the same code and a fresh file with just my company logo on (with all the image settings the same as Ben's), it fails.
If I can just resolve this and the borders vs. colspan issue, I'll be a hero! B->
</cliff>
Hi Cliff,
I am sorry that I could not remember because it was a way back to 2007. Anyway, I am using cfx excel to copy and modify the template. You can download at http://www.masrizal.com/index.cfm?fuseaction=idea.download_detail&ProductID=cfx_excel and try but it's limited. You need to purchase it for your company or for yourself if you want full functional custom tag?
Cheers
Eileen
@Cliff,
Have you tried opening up the template in Excel and then resaving it? Something that will fix things.
Has anyone experienced after writing updated data to a new Excel file when the resulting file is opened it says it is being accessed by another program and can only be opened read-only? I'm writing the file like Ben's example, is something else needed to "release" the file?
Thanks,
Jason
@Jason,
When you use some sort of file output stream, you *must* make sure to call .close() on the file stream to finalize the write otherwise the system will think it is still in use.
It looks like I am forgetting to do that in my example. If you look at my POI project page, the code there should probably do a better job of that.
hey Ben,
I followed this example and I am getting a strange error, for some reason it is not allowing me to modify the same row 2nd time, I get an error at
<cfset objRow = objSheet.GetRow(JavaCast("int", 19)) />
<cfset objCell = objRow.GetCell(JavaCast( "int", 3)) />
<cfset objCell.SetCellValue(JavaCast("string","aa")) />
and it says objCell is undefined, however if I change the row number to 20 or 18 it works fine, just because I update cell (row 19, col 2) and now cell (row 19, col 3) i get an error !
Any help highly appreciated.
Ben, how would one modify this to just update a specific column of data? My Excel template only need data within Column 7 from Row 3-8. My query display just six values, how can I then plug them into the template using your example?
I know there has been talk of using the POI to drop dynamic data into a spreadsheet and have the spreadsheet then display the data in a prefab chart but I'm having a bit of an issue getting that to work properly. I'm using Office 2007, and populating it with my dynamic data is working beautifully. I've already got a stacked bar chart working in my XLS template and technically it works once the data is loaded, provided you go into each of the fields being used and double click so that the spreadsheet can redo the math it will be using for the chart. This seems odd since the calculated fields are showing up correctly when the spreadsheet is downloaded but for whatever reason the chart refuses to use those initial calculated values to draw the graph. Any idea what I'm doing wrong or suggestions on what I might try next?
Hi Ben
I posted on one of the POI Tag pages about this and then found this post that shows how to loop through a template using the POI Utility , but now that we use the poi custom tags, wondering how you would use a template, replace out cells with tags (e.g. ~~Start Date~~~) with data from a database (array, list whatever) and then resave using the tags....
Thanks a lot as always for kicking ass!!
Matt
Ben
Certainly could have played around more before asking but found that the variable to save the workbook is set in the document end tag. I simply added to the "start" of the document tag..
cfif Len( ATTRIBUTES.Name )
cfset "CALLER.#ATTRIBUTES.Name#" = VARIABLES.Workbook
cfif
Then in the caller page you can manipulate the cells (change out tags for a template or find known rows/cells and then populate data) and then just close the </poi:document> and you have a new file with new data based off the old one using the custom tag (rather than poiUtility).
Hope this helps others and thanks for the tags once again.
Best,
Matt
I have used Aspose.Cells for Java Library for adding text in existing excel in java and the result was very satisfying.
http://www.aspose.com/java/excel-component.aspx