Converting Strings To Integers Using Hash, HashCode, And CRC-32 In ColdFusion
In my Feature Flags book, I had a snippet of code that uses the CRC-32 checksum in order to map strings to integers for user targeting. In his review of the book, Adam Cameron suggested that my code was longer than it needed to be; and, that I might use the hash() function for brevity. This gave me pause; especially in light of James Moberg's recent post on using .hashCode(). I want to take a moment and step back and think about how and why I'm converting strings to integers in ColdFusion.
The underlying mechanism of mapping a string onto an integer is a hashing function. A hashing function is any function that takes an input of arbitrary length and reduces it down an output with a predictable length. There are many different hashing algorithms, each of which is more-or-less suitable for any particular problem domain. The CRC-32 checksum, MD5 hash, and Java's String.hashCode() are all examples of hashing algorithms.
In the feature flags problem domain, mapping a string onto an integer is necessary when distributing a variant value using a percent-based rollout. For example, if you wanted to enable a feature flag for 5% of users, your feature flags SDK (Software Developer Kit) would need a way to determine if a given request falls into that 5% cohort or into the remaining 95% cohort. It does this by mapping the request key—which is a string—onto a numeric percentage (1-100).
This mapping of strings onto integers must be consistent across requests and across application reboots. If the mapping were inconsistent, a feature flag might be enabled for a user in one request and then mysteriously disabled for the same user in a subsequent request. This unpredictability would undermine the value-add of feature flags.
Furthermore, the mapping of strings onto integers should be evenly distributed on balance. This means that when I map a user's request key onto the 1-100 percentage integer, each value should roughly map to 1% of the overall user-base.
All to say, in the context of feature flags, I do not need a hashing function that is cryptographically secure. I only need a hashing function that is fast, consistent, and evenly distributed.
To play around with different mapping functions, I created an Encoder.cfc ColdFusion component that provides three methods for mapping arbitrary strings onto positive integers. Each method uses a different hashing algorithm: CRC-32, MD5, String.hashCode():
component
output = false
hint = "I provide various methods for encoding a string as an integer."
{
/**
* I initialize the encoder.
*/
public void function init() {
// Utility values to be used in methods.
variables.BigIntClass = createObject( "java", "java.math.BigInteger" );
variables.maxBigInt = BigIntClass.init( 2147483647 );
}
// ---
// PUBLIC METHODS.
// ---
/**
* I encode the given input using the Java native hashCode().
*/
public numeric function usingHashCode( required string input ) {
return( abs( javaCast( "string", input ).hashCode() ) );
}
/**
* I encode the given input using the ColdFusion native hash().
*/
public numeric function usingHash( required string input ) {
return BigIntClass
.init( hash( input ), 16 )
.mod( maxBigInt )
.intValue()
;
}
/**
* I encode the given input using a CRC-32 checksum.
*/
public numeric function usingCRC( required string input ) {
var checksum = createObject( "java", "java.util.zip.CRC32" )
.init()
;
checksum.update( charsetDecode( input, "utf-8" ) );
return BigIntClass
.valueOf( checksum.getValue() )
.mod( maxBigInt )
.intValue()
;
}
}
Since some of the hashing algorithms result in a value that can't be fit into a 32-bit integer, I'm using the modulo operator (in this case, .mod() method on BigInteger) to further reduce the value down to an integer.
The CRC-32 and MD5 algorithms are consistent by design. The String.hashCode() method is a bit more contentious. In the Java documentation of Object.hashCode(), it says that:
Whenever it is invoked on the same object more than once during an execution of a Java application, the hashCode method must consistently return the same integer, provided no information used in equals comparisons on the object is modified. This integer need not remain consistent from one execution of an application to another execution of the same application.
However, if you look at the overridden method in the String class, it explicitly defines the algorithm for hashing the string:
Returns a hash code for this string. The hash code for a String object is computed as:
s[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]
What I take this to mean is that while the more generic Object.hashCode() is unpredictable across systems, String.hashCode() is predictable across systems. And, in fact, this is what James Moberg saw in his exploration as well (see earlier link).
Assuming consistent mapping, I'm still curious to explore speed and distribution. For speed, I'm going to see how many times I can execute each algorithm in 3 seconds. For the input, I'm using a distinct value that looks like an IP address (so as to more closely mirror what I might use in a real world application):
<cfscript>
encoder = new Encoder();
maxDuration = 3000;
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
count = runFor(
( i ) => {
return( encoder.usingHashCode( "#i#.192.#i#.168.#i#" ) );
},
maxDuration
);
echoLine( "HashCode: #numberFormat( count )#" );
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
count = runFor(
( i ) => {
return( encoder.usingHash( "#i#.192.#i#.168.#i#" ) );
},
maxDuration
);
echoLine( "Hash: #numberFormat( count )#" );
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
count = runFor(
( i ) => {
return( encoder.usingCRC( "#i#.192.#i#.168.#i#" ) );
},
maxDuration
);
echoLine( "CRC-32: #numberFormat( count )#" );
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
/**
* I run the given operator as many times as I can in the given duration.
*/
public numeric function runFor(
required function operator,
required numeric durationInMilliseconds
) {
var cutoffAt = ( getTickCount() + durationInMilliseconds );
var executionCount = 0;
while ( getTickCount() < cutoffAt ) {
operator( ++executionCount );
}
return( executionCount );
}
/**
* I output the given value followed by a BR tag.
*/
public void function echoLine( string value = "" ) {
writeOutput( value & "<br />" );
}
</cfscript>
If I run this in Lucee CFML, I get the following output:
- HashCode: 18,981 (oddly slow!)
- Hash: 166,875
- CRC-32: 516,026
And, if I run this in Adobe ColdFusion, I get the following output:
- HashCode: 645,021
- Hash: 414,450
- CRC-32: 265,481
It's strange that the two different CFML engines have inverse speed outcomes. This could be something in the way I'm calling the code; or, it could be something in the engine implementations.
It's particularly strange how much slower String.hashCode() seems to be in Lucee CFML for my particular inputs. This is a Java-layer method call; and, both of my local CommandBox servers appear to be using Java 11.0.21 (Homebrew) 64bit. As such, I have to imagine that there's something funky in my code that is just not obvious.
That said, these methods are all pretty fast (bar that one oddity). So, let's look at the distribution of inputs onto outputs. As I mentioned above, in a feature flags context, we need to map user key values onto 1-100 percentage buckets. As such, I'm going to use the modulo operator (%) to further reduce each value:
<cfscript>
encoder = new Encoder();
iterations = 100000;
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
buckets = [];
arraySet( buckets, 1, 100, 0 );
for ( i = 1 ; i <= iterations ; i++ ) {
encodedInt = encoder.usingHashCode( "#i#.192.#i#.168.#i#" );
bucketIndex = ( ( encodedInt % 100 ) + 1 );
buckets[ bucketIndex ]++;
}
printBuckets( "Using Hash Code", buckets );
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
buckets = [];
arraySet( buckets, 1, 100, 0 );
for ( i = 1 ; i <= iterations ; i++ ) {
encodedInt = encoder.usingHash( "#i#.192.#i#.168.#i#" );
bucketIndex = ( ( encodedInt % 100 ) + 1 );
buckets[ bucketIndex ]++;
}
printBuckets( "Using Hash", buckets );
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
buckets = [];
arraySet( buckets, 1, 100, 0 );
for ( i = 1 ; i <= iterations ; i++ ) {
encodedInt = encoder.usingCRC( "#i#.192.#i#.168.#i#" );
bucketIndex = ( ( encodedInt % 100 ) + 1 );
buckets[ bucketIndex ]++;
}
printBuckets( "Using CRC-32", buckets );
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
/**
* I output the buckets as a horizontal bar-chart.
*/
public void function printBuckets(
required string title,
required array buckets
) {
```
<cfoutput>
<div style="float: left ; margin-right: 20px ;">
<h2>
#encodeForHtml( title )#
</h2>
<cfloop index="local.value" array="#buckets#">
<div
style="background: hotpink ; width: #( value / 4 )#px ; height: 4px ;">
</div>
</cfloop>
</div>
</cfoutput>
```
}
</cfscript>
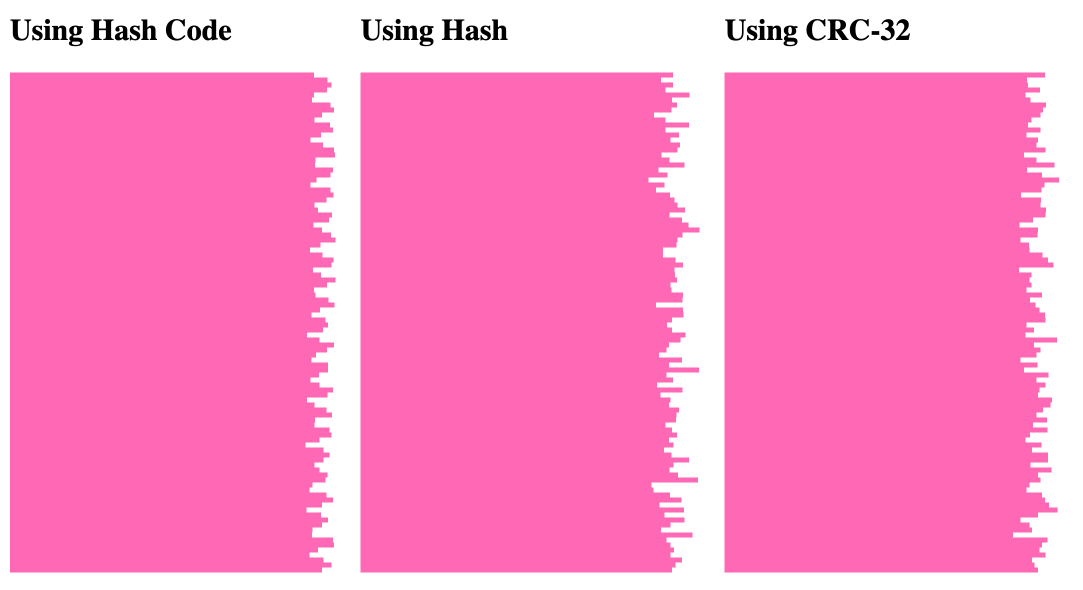
This just keeps a running tally of how many times each bucket index is generated over 100,000 iteration. And then, plots it as a horizontal bar chart:
As you can see, each of the hashing algorithms gives us a "good enough" distribution, on balance.
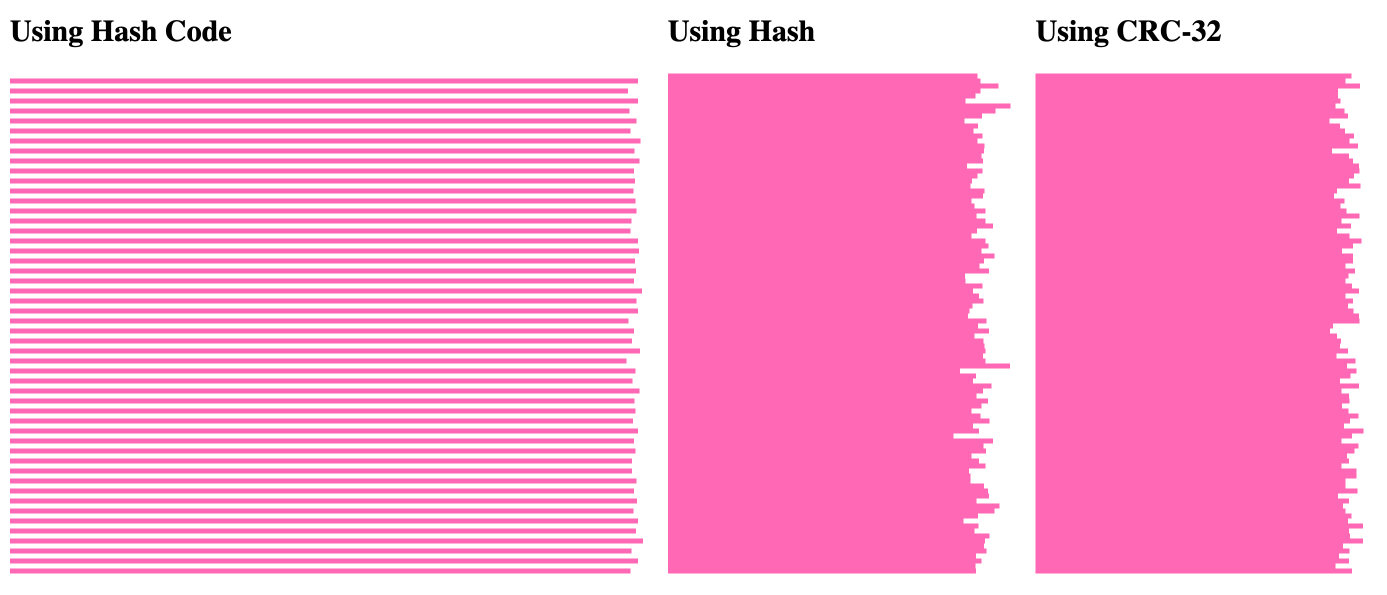
That said, I accidentally noticed something really strange! When running the distribution code, if I change the input from:
"#i#.192.#i#.168.#i#"
to:
"192.#i#.168.#i#"
(notice that I've removed the leading #i#.), it radically alters the distribution for the String.hashCode() execution:
Here, it seems that every other percentage bucket in the String.hashCode() algorithm is 0. Meanwhile, the other two hashing algorithms continue to have an evenly distributed mapping.
I'm not sure what is going on here; but, it must have something to do with the fact that the leading characters in this latter execution are always the same (192.); which must have an outsized impact on the overall hash code generation. I'm glad to have accidentally stumbled upon this strange outcome.
In the end, I'll probably just stick with the CRC-32 hashing algorithm as the example in the book. The String.hashCode() would have been the nicest approach to use because it's so simple; but, I don't want to lead people down the wrong path. Still, it was good to step back and think more deeply about why I'm mapping strings to integers and how I'm choosing to do that.
Want to use code from this post? Check out the license.

Reader Comments
Over on Twitter, James Moberg demonstrates that you can use the
.hashCode()approach to get an even distribution if you approach the problem slightly differently. Whereas I'm basically doing this:abs( .hashCode() ) % 100... he checks to see where the value falls within the total range of values. Assume for a moment that
Nis "max integer" value. He's doing this:( .hashCode() + N ) / 2N * 100Basically,
.hashCode()generates a value between-N..N. His math adds a max integer to convert the range to0..2N. Then, he divides by2Nto see where the hash-code value falls, percentage-wise, in the0..2Nrange. He then multiplies that by the number of buckets (100).This works. I tried to simplify it on my end by doing:
( .hashCode() + N ) % 100... but, my simplification does not work well for the distribution. I don't understand the math theory here well enough to know why the modulo-approach is different than the percent-approach.
Post A Comment — ❤️ I'd Love To Hear From You! ❤️
Post a Comment →