Templates Appear To Maintain Lexical Bindings In Angular 2 RC 1
Yesterday, when I was experimenting with dynamic template rendering in Angular 2, I happend to notice that the ngFor directive can accept an external TemplateRef. Not only did I want to experiment with this ngFor feature; but, it got me generally thinking about how a template maintains its bindings when its passed out-of-scope. From what I can see, it looks like a TemplateRef maintains the lexical binding to both its defining View and its defining Component instance.
Run this demo in my JavaScript Demos project on GitHub.
To explore this idea, I created a completely trite component that does nothing more than proxy an ngFor directive. It accepts an [items] input and a [template] input and then uses both of these bindings to render an ngFor list.
// Import the core angular services.
import { Component } from "@angular/core";
import { TemplateRef } from "@angular/core";
@Component({
selector: "item-list",
inputs: [ "items", "template" ],
// In this View, notice that we are passing in a [ngForTemplate] to our ngFor
// directive. In doing so, the ngFor directive will use this template for rendering
// instead of its own TemplateRef.
// --
// NOTE: The ngFor directive will still use the same context object when rendering
// the externally-provided TemplateRef. As such, the external template can still use
// local view variables like "let-index" and "let-even".
template:
`
<ul>
<template ngFor [ngForOf]="items" [ngForTemplate]="template"></template>
</ul>
`
})
export class ItemListComponent {
// I hold the collection of items to render.
// --
// NOTE: Injected input value.
public items: any[];
// I hold the externally provided TemplateRef to render in the ngFor repeater.
// --
// NOTE: Injected input value.
public template: TemplateRef<any>;
// I initialize the component.
constructor() {
// ... nothing to do here.
}
}
Notice that the ngFor directive is accepting an [ngForTemplate] property. Internally, the ngFor directive will then use this passed-in TemplateRef input instead of its own dependency-injected TemplateRef when creating the embedded views.
In the root component, I then defined a <template> element and gave it a view-local reference that I could pass into the ItemListComponent. In the following code, take a careful look at what I'm referencing from within the template.
// Import the core angular services.
import { Component } from "@angular/core";
// Import the application components and services.
import { ItemListComponent } from "./item-list.component";
export interface IFriend {
id: number;
name: string;
};
@Component({
selector: "my-app",
directives: [ ItemListComponent ],
// In the following view, we're defining a TemplateRef and then passing it into the
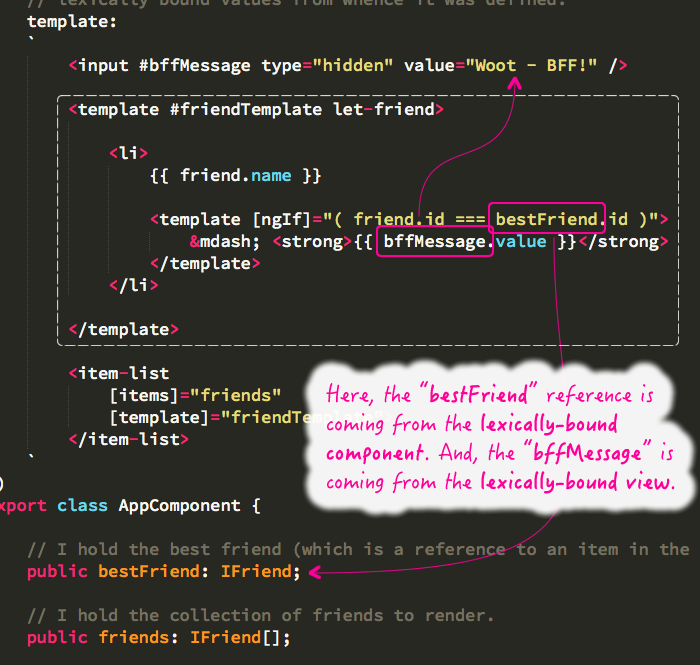
// <item-list> component. Notice, however, that the template is making references to
// both local-view values (ie, let-X) as well as lexically-bound values to the root
// component (ie, this.bestFriend) and the component template (ie, #bffMessage). Even
// when the TemplateRef gets passed out-of-scope, it can still reference the
// lexically-bound values from whence it was defined.
template:
`
<input #bffMessage type="hidden" value="Woot - BFF!" />
<template #friendTemplate let-friend>
<li>
{{ friend.name }}
<template [ngIf]="( friend.id === bestFriend.id )">
— <strong>{{ bffMessage.value }}</strong>
</template>
</li>
</template>
<item-list
[items]="friends"
[template]="friendTemplate">
</item-list>
`
})
export class AppComponent {
// I hold the best friend (which is a reference to an item in the collection).
public bestFriend: IFriend;
// I hold the collection of friends to render.
public friends: IFriend[];
// I initialize the component.
constructor() {
this.friends = [ "Sarah", "Kim", "Tricia", "Lisa", "Joanna" ].map(
function iterator( name: string, index: number ) : IFriend {
return({
id: index,
name: name
});
}
);
this.bestFriend = this.friends[ 1 ];
}
}
As you can see, not only am I using the view-local variables exposed by the ngFor directive context (ex, let-friend), I'm also referencing a sibling element (#bffMessage) and a property on the root component itself (this.bestFriend).
When we run this code, everything just works. Seamlessly.

This is really quite awesome. Especially since we can pass templates into other components for dynamic rendering. The fact that those passed-in templates maintain lexical binding to their defining components makes them much more usable.
Want to use code from this post? Check out the license.

Reader Comments
@Ben,
Cool stuff!
This idea (minus local template variables) was possible in angular 1 too.
Basically it doesn't matter what is the source of the lexical bind, view or component, it's a mechanism to bind properties from the "outside world"
In angular 1, you would have used a directive and $compile it with a $scope, since you can move objects around the $scope can be anything, same behaviour.
In Angular 2 templates are a first class citizen with their a special component (<template>) which makes things works a bit different but with same outcome.
Also, in angular 2 the compiler was abstracted away, to support offline compilation so we can't do it the old way (and also can't create NEW component types dynamically.)
So is this just like passing a function to another function?
I mean that when that passed function being executed, it executes in a context it was defined, but also is able to accept some other data via arguments from the execution context.
@Shlomi,
Right, good point. It's actually been a while since I've played with NG1 (since reading up on all this NG2 stuff); so, my mental model is starting to slip. I know that when you set the "transclude: true | element", the content of the component was pre-compiled and linked to the lexical scope... and then provided to your component as a packaged linking function .... or something like that :D I don't remember all the details off hand.
The <template> stuff in NG2 is pretty cool. Especially now that I'm starting to understand how much of a first-class citizen it is.
@Anton,
Yeah, I think that is a pretty legitimate comparison. The template maintains the lexical bindings. However, when the ViewContainerRef needs to clone / insert the template instances, it can provide a "context" variable that exposes "let-enabled" values as well.
Hi Ben,
have You been trying to provide data binding in standard way (angular templating) for dynamically created components?
so, there is a very long discussion about it https://github.com/angular/angular/issues/6223 and just to minimize your time for reading all that lagacy stuff i show an example which is the only one way (IMO) to do that but only to dyrectly setting a Component instance properties - https://github.com/angular/angular/issues/6223#issuecomment-221940268
i wanna hope that there is some more simple and abstract way to automatically setup dynamically created component's @Input an @Output properties for data binding targets and sources... what do You think about it ?
@Max,
I haven't played around with the Dynamic Component Loader yet. I briefly looked at it when investigating this problem; but, it didn't seem to be right fit, especially since I need to render an arbitrary template. As such, the ViewContainerRef / TemplateRef approach ended up being the right one.
Thanks for the link, though - it is something I plan to investigate.
Hi Ben,
I'm trying to find ways to load a template from some sort of external source, in our case it will be from external files.
All the examples I have seen around dynamic components, templates, templateRefs etc involve defining the template either in a separate html file referenced by the templateUrl attribute or inline using the template attribute on a Component.
Can you inject the template as a string into a component, and have data binding?