Ask Ben: Recursive Numeric Pyramid
Can you help me to find solution of this question by the recursion just print on the screen:
0
0 1
0 1 2
0 1 2 3
0 1 2 3 4
0 1 2 3
0 1 2
0 1
0Thanx alot and help me to understand recursion very well. Thanx alot.
I am glad that this particular question was asked because this is not necessarily a case where recursion is the best answer. When you're learning recursion, just as when you learn anything new, you start to see it as solution to problems that don't necessarily need it. Sometimes that's because recursion just feels right; sometimes that's because patterns in problems are just straight-up hard to see.
In this case, the pattern is that the height of each row (number of columns in that row) is directly related to the difference between the max height and the absolute value of the current row when placed on a graph where the max row falls on the (y=0) axis. To better see this, take a look at this graphic:
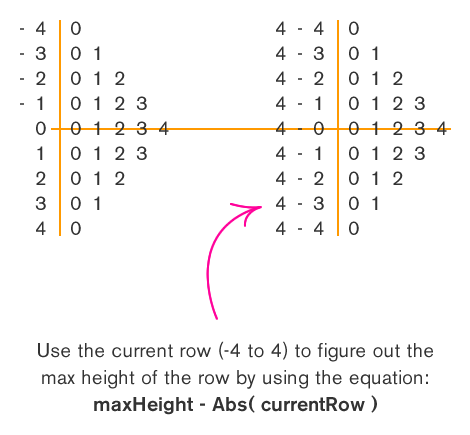
With that in mind, this problem can be solved using two nested FOR loops:
<!--- Get the max height of the numeric pyramid. --->
<cfset intHeight = 4 />
<!---
Loop over the number of rows that we want to display
in our numeric pyramid. This will start at negative
*height* and go to positive *height*. This will give
us ((height * 2) + 1) rows.
--->
<cfloop
index="intRow"
from="#-intHeight#"
to="#intHeight#"
step="1">
<!---
Loop over the number of columns in this row,
starting at zero.
--->
<cfloop
index="intCol"
from="0"
to="#(intHeight - Abs( intRow ))#"
step="1">
#intCol#
</cfloop>
<!--- Line break. --->
<br />
</cfloop>
As you can see, we just loop from -intHeight to intHeight and output each appropriate column. This has a very linear execution path to it and it is completely scalable and will work no matter what the max height of the pyramid is.
That being said, you can also solve this problem using recursion, but you will quickly see that the recursive method has a lot more overhead in terms of both code and general logic. When it comes to recursion, one aspect of it can be thought of as a divide and conquer problem; for each iteration, we are solving a small part of the problem and then handing off the rest of it to be solved separately by the same function.
With that in mind, what is the divide and conquer approach to a pyramid? When I look at it, I see a mirror image reflected around the row with the max height. Taking that and extrapolating it to a divide and conquer approach, we want to output the smallest rows (top 0 and bottom 0) and then output everything in between those two rows. As we output everything between those two rows, we are going to output the top 0-1 row and the bottom 0-1 row and then everything in between those two rows... and so on and so forth until we hit our point of reflection - the max row.
Let's take that idea and wrap it up in a recursive function:
<cffunction
name="OutputPyramid"
access="public"
returntype="void"
output="true"
hint="Outputs the numeric pyramid.">
<!--- Define arguments. --->
<cfargument
name="TargetHeight"
type="numeric"
required="true"
hint="The max height of the numeric pyramid."
/>
<cfargument
name="CurrentHeight"
type="numeric"
required="false"
default="0"
hint="The current height of the output pyramid."
/>
<!--- Define the local scope. --->
<cfset var LOCAL = StructNew() />
<!---
Check to see if the current height is equal to the
target height. In that case, we are going to output
just one row.
--->
<cfif (ARGUMENTS.TargetHeight EQ ARGUMENTS.CurrentHeight)>
<!--- Simply output the row to max height. --->
<cfloop
index="LOCAL.Column"
from="0"
to="#ARGUMENTS.TargetHeight#"
step="1">
#LOCAL.Column#
</cfloop>
<br />
<cfelse>
<!---
Since we are not outputting the max height row, we
want to output TWO of the same column sets with a
recursive call in the middle.
--->
<!--- Output first row. --->
<cfloop
index="LOCAL.Column"
from="0"
to="#ARGUMENTS.CurrentHeight#"
step="1">
#LOCAL.Column#
</cfloop>
<br />
<!---
In between our two mirrow columns, we want to output
the middle content. These are the rows with heigher
columns (and eventually the one max row). To make
this recursive, make sure to re-call this method
with a larget current row.
--->
<cfset OutputPyramid(
TargetHeight = ARGUMENTS.TargetHeight,
CurrentHeight = (ARGUMENTS.CurrentHeight + 1)
) />
<!--- Output second row (same as first). --->
<cfloop
index="LOCAL.Column"
from="0"
to="#ARGUMENTS.CurrentHeight#"
step="1">
#LOCAL.Column#
</cfloop>
<br />
</cfif>
<!--- Return out. --->
<cfreturn />
</cffunction>
As you can see, in our function we have two cases: either we are outputting the max row or we are outputting the two smaller columns on either side of the max row. Remember, it is essential to have logic in your recursive function that allows it to eventually execute without re-invoking itself. In our case, that scenario is the max row output. Notice that when we output the max row, we do not re-invoke the OutputPyramid() function. It is only when we are outputting the smaller rows that we re-execute the OutputPyramid() method to output the content between the two smaller rows.
Once we have this recursive function in place, we simply need to invoke it with the target height of the numeric pyramid:
<!--- Output a numeric pyrmaid with max height of 4. --->
<cfset OutputPyramid( 4 ) />
Since the current row height defaults to 0, that will be implied in our launch code.
Not only is there much more code involved in the recursive solution to this problem, there is also a lot of duplicate logic. We have three FOR loops; two of which do the exact same thing (output the smaller rows) but all three of them perform pretty much the same task - output from 0 to a specified height. There is a way to consolidate much of the code, but then you pretty much end up re-creating the original solution wrapped up in the overhead of a recursive function. So, recursion is an awesome thing, but certainly, not always the best option.
Want to use code from this post? Check out the license.

Reader Comments
Hi Ben,
Here is another take, which only needs one loop:
<!--- set up our variables ---->
<cfset pSize = 4>
<cfset currNum = 0>
<cfset retString = ''>
<cfset pyramid = ''>
<!--- Here is our recursive function --->
<cffunction name='buildPyramid' returntype="string">
<cfargument name="pDir" type="string" required="true">
<cfloop from=0 to=#currNum# index='x'>
<cfset retString = "#retString# #x#">
</cfloop>
<cfset retString = "#retString#<br>">
<cfif currNum LT pSize AND pDir EQ 'up'>
<cfset currNum = currNum + 1>
<cfset pyramid = buildPyramid('up')>
<cfelseif currNum GT 0>
<cfset currNum = currNum - 1>
<cfset pyramid = buildPyramid('down')>
</cfif>
<cfreturn retString>
</cffunction>
<!--- call the function --->
<cfset pyramid = buildPyramid('up')>
<!--- output the result --- >
<cfoutput>#pyramid#</cfoutput>
@Gus,
Good stuff. Even with one loop, though, I think we see that the non-recursive solution is more simplistic. Also, I would try to pass variables through with the method calls rather than refer to global variables (that just makes me feel a bit uncomfortable).
OK, I had to try :)
No loops, recursion only (perhaps not completely the best method, but appears to work correctly) and I had to use the dreaded...*evaluate* :D BTW, this sounded quite a bit like a homework assignment, but I quite enjoyed the small challend.
<cffunction name="recurse" access="remote" output="true" returntype="void">
<cfargument name="currentValue" default="0" type="numeric" />
<cfargument name="maxValue" default="4" type="numeric" />
<cfargument name="direction" default="+" type="string" />
<cfargument name="arrayValue" default="#arrayNew(1)#" type="array" />
<cfif arguments.currentValue gt -1>
<cfif arguments.direction is "+">
<cfset arrayAppend(arguments.arrayValue, arguments.currentValue)>
<cfelseif arrayLen(arguments.arrayValue)>
<cfset arrayDeleteAt(arguments.arrayValue, arrayLen(arguments.arrayValue))>
</cfif>
<cfoutput>#ArrayToList(arguments.arrayValue, " ")#</cfoutput><br>
<cfif arguments.currentValue eq arguments.maxValue>
<cfset arguments.direction = "-">
</cfif>
<cfset recurse(Evaluate("arguments.currentValue" & arguments.direction & "1"), arguments.maxValue, arguments.direction, arguments.arrayValue) >
</cfif>
</cffunction>
@Gareth,
Nicely done. I like how you are using the direction variable to work also as a mathematical operator. As far as the Evaluate() goes, you can actually do that without using it:
Evaluate("arguments.currentValue" & arguments.direction & "1")
... can simply be:
arguments.currentValue + "#arguments.direction#1"
In this case, you are creating a string form of a number (+1 or -1) and then adding that to the currentValue. ColdFusion will convert the string to a number for you (in theory - I have not tested).
Yeah, it did feel like a homework question :)
Here's my take. Comments are welcome.
<cfscript>
min = 0;
max = 4;
// code: http://shayne.pastebin.com/f9f28c41
myCounter = CreateObject("component", "Counter").init(min,max);
myCounter.setDelimiter(" ");
for (i=min; i <= max; ++i) {
myCounter.setEndNum(max-i);
WriteOutput(myCounter.run() & "<br />");
}
for (i=min+1; i <= max; ++i) {
myCounter.setEndNum(i);
WriteOutput(myCounter.run() & "<br />");
}
</cfscript>
@Shayne,
Geez that's a lot of code :) Not sure that the extra overhead for creating the object would be worth it, but the way you've written it is definitely a lot more extensible than mine would be :)
I managed to revise the code slightly and get rid of my evaluate completely
<cffunction name="recurse" access="remote" output="true" returntype="void">
<cfargument name="direction" default="+" type="string" />
<cfargument name="arrayValue" default="#arrayNew(1)#" type="array" />
<cfset var maxValue = 5 />
<cfif arguments.direction is "+">
<cfset arrayAppend(arguments.arrayValue, arrayLen(arguments.arrayValue))>
<cfelseif arrayLen(arguments.arrayValue)>
<cfset arrayDeleteAt(arguments.arrayValue, arrayLen(arguments.arrayValue))>
</cfif>
<cfif arrayLen(arguments.arrayValue)>
<cfoutput>#ArrayToList(arguments.arrayValue, " ")#</cfoutput><br>
<cfif arrayLen(arguments.arrayValue) eq maxValue>
<cfset arguments.direction = "-">
</cfif>
<cfset recurse(arguments.direction, arguments.arrayValue) >
</cfif>
</cffunction>
@Gareth
Yeah - I took a different approach to the problem. Not so say which is better, faster, stronger, etc... (daft punk anyone?).
Warning! My opinion: I don't think the few milliseconds it takes to create the object would warrant the need to implement something procedurally, inline. I'm sure there are a few situations that would favor something procedural - in regards to speed. Given the amount of re-usability and maintainability OO designs offer - I tend to look in that direction. You never know when you might need to generate a linear numeric sequence!
@Shayne,
Cool take on it. I like that you package up the row building logic into the CFC.
@Gareth,
Way to get rid of the Evaluate; more than that, though, that seems like a cleaner solution. The one minor note - if you have have output="true" in your CFFunction tag, you don't need the CFOutput tags.
Good stuff.
@Ben,
I've never tried leaving out the cfoutput tags when setting output="true". Nice!
@Gareth,
No problem. Yeah, when you define the function tag as being output, the whole body of the function acts as though it were inside a CFOutput tag (like being inside CFMail).