Considering Ways To Embed Widgets In My Markdown Using Flexmark 0.42.6 And ColdFusion
As I mentioned yesterday, I am trying to move my publishing workflow over from an ActiveX context (that requires me running XStandard in IE 11 on a Windows Virtual Machine) to a Markdown context that uses Flexmark 0.42.6 and ColdFusion. Markdown is fairly powerful when it comes to authored content. But, it doesn't really have any mechanism for embedded "widgets" like Vimeo or YouTube videos. Flexmark does allow you to write Extensions for the Markdown parser (ex, the "YouTube Embedded Link Transformer"); but, that's quite a bit beyond my experience level. As such, I wanted to look at ways I could use some Regular Expression (RegEx) parsing to embed widgets as part of a post-processing step in the Markdown-to-HTML conversion.
View this code in my Flexmark-0.42.6-With-ColdFusion project on GitHub.
First, I should say that embedding a widget in Markdown doesn't necessarily require any additional steps. This is because you can embed HTML right in your markdown content. As such, if I wanted to embed a Vimeo video into an article, I could just go to Vimeo, copy the iframe code for a given video, and then paste it right into my markdown. This is totally valid.
But, the downside to this approach is that it tightly couples the intent of the widget - "embed a video" - to the implementation of the widget - "use this iframe". It also requires a lot more syntax, which makes it more prone to error and inconsistency. And, if we ever wanted to change the implementation, we'd have to get down-and-dirty with some potentially complex Regular Expression find-and-replace operations.
To keep things flexible, I want to noodle on some ways in which I could embed an "abstraction" for a widget in my Markdown rather than an implementation. This way, if I ever need to change the implementation of a particular widget, all I would have to do is re-process the markdown.
First, I started with considering the author ergonomics. Meaning, as a content publisher, what would "feel good" to use in my markdown? Ultimately, the most straightforward ideas that I came up with were to use an HTML Comment or a Script tag, both of which can be embedded as-is in Flexmark markdown:
When it comes to embedding widgets in my markdown, I could just embed the HTML
right in the content. Embedding HTML is a totally valid approach:
<iframe
src="//player.vimeo.com/video/96794772?color=ff3366"
width="700"
height="394"
frameborder="0"
webkitallowfullscreen
mozallowfullscreen
allowfullscreen
></iframe>
The problem with this is that tightly couples the "intent" of the widget to the
"implementation" of the widget. Plus, it's quite verbose. Instead, what I'd like
to do is provide a _description_ of the widget; and then hide the implementation
behind some sort of post-processing.
The first approach that I thought of was to use an HTML Comment to embed simple
markers that could be replaced with a RegEx pattern:
<!-- vimeo: 96794772 -->
The above approach is nice when there is a single token to work with (such as
the video ID) because the pattern is really easy to match. But, if the data is
more complex and has several attributes, it might be nice to work with a complex
data structure. For this, I could use a Script tag to embed JSON (JavaScript
Object Notation) directly in the content:
<script type="markdown/widget">
{
"type": "vimeo",
"vimeo": {
"id": "96794772",
"color": "ffffff"
}
}
</script>
In this case, we're still using a RegEx pattern to match the payload between the
open `<script>` and the close `</script>`. But, the contents ultimately get
parsed using the `deserializeJson()` function.
But, then I wondered, could I just do the same thing with an HTML Comment and a
bit less ceremony:
<!-- json:
{
"type": "vimeo",
"vimeo": {
"id": "96794772",
"color": "ff00ff"
}
}
-->
This approach works quite well and has less syntax. But, isn't quite as
attractive, visually speaking. That said, any of these approach is sufficient
and fills me with hope that migrating to Markdown will be easier than I thought
it would be.
As you can see, both the HTML Comments and the Script tags are providing an abstraction - they aren't describing the widget implementation, they are merely describing what kind of widget to embed. The actual implementation will be applied in a post-processing step of the Markdown-to-HTML conversion.
And, to help with this post-processing, I'm going to use my JRegEx ColdFusion component. The JRegEx component allows for - among other things - easy, closure-based application of patterns and text-replacements.
With that said, here's the ColdFusion code that loads Flexmark, pulls in the markdown file, and then replaces the widget "markers" with the actual widget implementations:
<cfscript>
// Read-in our markdown file.
markdown = fileRead( expandPath( "./widgets.md" ) );
// Create some of our Class definitions. We need this in order to access some static
// methods and properties.
HtmlRendererClass = application.flexmarkJavaLoader.create( "com.vladsch.flexmark.html.HtmlRenderer" );
ParserClass = application.flexmarkJavaLoader.create( "com.vladsch.flexmark.parser.Parser" );
// Create our parser and renderer - both using the options.
options = application.flexmarkJavaLoader.create( "com.vladsch.flexmark.util.options.MutableDataSet" ).init();
parser = ParserClass.builder( options ).build();
renderer = HtmlRendererClass.builder( options ).build();
// Parse the markdown into an AST (Abstract Syntax Tree) document node.
document = parser.parse( javaCast( "string", markdown ) );
// Render the AST (Abstract Syntax Tree) document into an HTML string.
html = renderer.render( document );
// The JRegEx component will help us parse and replace the resultant HTML.
jre = new JRegEx();
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
// This version replaces the simple Vimeo VideoID widget.
html = jre.jreReplace(
html,
"<!-- vimeo: *(\S+) -->",
function( $0, videoID ) {
// NOTE: I am including the original captured group in the output ($0) in
// order to make the inputs and outputs easier to see in the demo.
return('
#$0#
<iframe
src="//player.vimeo.com/video/#videoID#?color=ff0179"
width="700"
height="394"
frameborder="0"
webkitallowfullscreen
mozallowfullscreen
allowfullscreen
></iframe>
');
}
);
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
// This version replaces the more complex Script tag containing JSON content.
html = jre.jreReplace(
html,
"<script type=.markdown/widget.>([\S\s]+?)</script>",
function( $0, json ) {
var data = deserializeJson( trim( json ) );
// NOTE: I am including the original captured group in the output ($0) in
// order to make the inputs and outputs easier to see in the demo.
return('
#$0#
<iframe
src="//player.vimeo.com/video/#data.vimeo.id#?color=#data.vimeo.color#"
width="700"
height="394"
frameborder="0"
webkitallowfullscreen
mozallowfullscreen
allowfullscreen
></iframe>
');
}
);
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
// This version replaces JSON, but using an HTML Comment instead of a Script tag.
html = jre.jreReplace(
html,
"<!--\s*json:([\S\s]+?)-->",
function( $0, json ) {
var data = deserializeJson( trim( json ) );
// NOTE: I am including the original captured group in the output ($0) in
// order to make the inputs and outputs easier to see in the demo.
return('
#$0#
<iframe
src="//player.vimeo.com/video/#data.vimeo.id#?color=#data.vimeo.color#"
width="700"
height="394"
frameborder="0"
webkitallowfullscreen
mozallowfullscreen
allowfullscreen
></iframe>
');
}
);
// ------------------------------------------------------------------------------- //
// ------------------------------------------------------------------------------- //
</cfscript>
<!doctype html>
<html lang="en">
<head>
<meta charset="utf-8" />
<title>
Considering Ways To Embed Widgets In My Markdown Using Flexmark 0.42.6 And ColdFusion
</title>
</head>
<body>
<h1>
Considering Ways To Embed Widgets In My Markdown Using Flexmark 0.42.6 And ColdFusion
</h1>
<h2>
Rendered Output:
</h2>
<hr />
<cfoutput>#html#</cfoutput>
<hr />
<h2>
Rendered Markup:
</h2>
<pre class="language-html"
><code class="language-html"
><cfoutput>#encodeForHtml( html )#</cfoutput
></code
></pre>
<!-- For our fenced code-block syntax highlighting. -->
<link rel="stylesheet" type="text/css" href="./vendor/prism-1.14.0/prism.css" />
<script type="text/javascript" src="./vendor/prism-1.14.0/prism.js"></script>
</body>
</html>
As you can see, this approach doesn't extend the Flexmark parser - it simply applies additional string-manipulation to the HTML produced by the Flexmark renderer. This allows the markdown snippet:
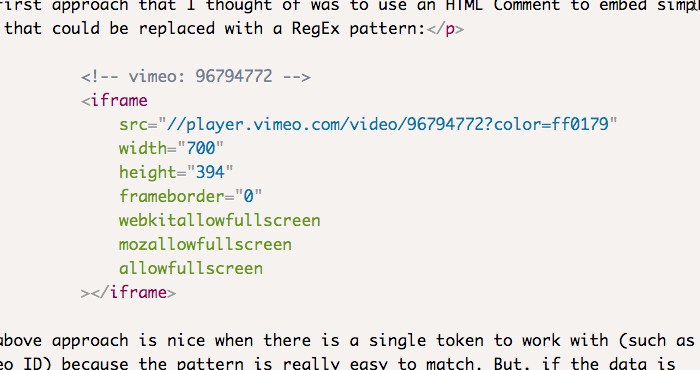
<!-- vimeo: 96794772 -->
... to be rendered in HTML like this:
And, for the sake of completeness, here's the full HTML output:
NOTE: I've removed some of the indentation that was added by my RegEx string manipulation.
<p>When it comes to embedding widgets in my markdown, I could just embed the HTML
right in the content. Embedding HTML is a totally valid approach:</p>
<iframe
src="//player.vimeo.com/video/96794772?color=ff3366"
width="700"
height="394"
frameborder="0"
webkitallowfullscreen
mozallowfullscreen
allowfullscreen
></iframe>
<p>The problem with this is that tightly couples the "intent" of the widget to the
"implementation" of the widget. Plus, it's quite verbose. Instead, what I'd like
to do is provide a <em>description</em> of the widget; and then hide the implementation
behind some sort of post-processing.</p>
<p>The first approach that I thought of was to use an HTML Comment to embed simple
markers that could be replaced with a RegEx pattern:</p>
<!-- vimeo: 96794772 -->
<iframe
src="//player.vimeo.com/video/96794772?color=ff0179"
width="700"
height="394"
frameborder="0"
webkitallowfullscreen
mozallowfullscreen
allowfullscreen
></iframe>
<p>The above approach is nice when there is a single token to work with (such as
the video ID) because the pattern is really easy to match. But, if the data is
more complex and has several attributes, it might be nice to work with a complex
data structure. For this, I could use a Script tag to embed JSON (JavaScript
Object Notation) directly in the content:</p>
<script type="markdown/widget">
{
"type": "vimeo",
"vimeo": {
"id": "96794772",
"color": "ffffff"
}
}
</script>
<iframe
src="//player.vimeo.com/video/96794772?color=ffffff"
width="700"
height="394"
frameborder="0"
webkitallowfullscreen
mozallowfullscreen
allowfullscreen
></iframe>
<p>In this case, we're still using a RegEx pattern to match the payload between the
open <code><script></code> and the close <code></script></code>. But, the contents ultimately get
parsed using the <code>deserializeJson()</code> function.</p>
<p>But, then I wondered, could I just do the same thing with an HTML Comment and a
bit less ceremony:</p>
<!-- json:
{
"type": "vimeo",
"vimeo": {
"id": "96794772",
"color": "ff00ff"
}
}
-->
<iframe
src="//player.vimeo.com/video/96794772?color=ff00ff"
width="700"
height="394"
frameborder="0"
webkitallowfullscreen
mozallowfullscreen
allowfullscreen
></iframe>
<p>This approach works quite well and has less syntax. But, isn't quite as
attractive, visually speaking. That said, any of these approach is sufficient
and fills me with hope that migrating to Markdown will be easier than I thought
it would be.</p>
At this point, I feel like I have all the ingredients that I need in order to move my content publishing workflow over to Markdown. The only thing that I'll really be losing is the automatic application of Image dimensions (width and height). But, I do know that I can use the Attributes Extension in Flexmark to provide the image dimensions explicitly in my markdown. This poses a small degree of friction; but, one that I am completely willing to live with.
Want to use code from this post? Check out the license.

Reader Comments
Ben. Good to see you back on the Coldfusion!
So, what stuck out like a sore thumb was:
What is this? So, it looks like some kind of Regex magic?
And I see that the 3rd parameter can be a function.
Can you explain how this part works?
I think the posting mechanism went AWOL. Sorry for the repeats. Not sure why that happened...
@Charles,
Sorry about that. I think sometimes the POST fails and I must not be trapping the error properly. I have it on my list of things to look at. Probably just a silly oversight somewhere.
JRegEx is a ColdFusion component that I wrote that wraps around the Java classes for
PatternandMatcher:https://github.com/bennadel/ColdFusion-JRegEx
Some of the methods allow straight string-replacement. But, some methods, like the
.jreReplace()method take a Function as the last argument. I modeled this after the concept of the JavaScript.replace()method, which can take a Function that accepts the matched-groups and returns the replacement.ColdFusion has some decent Pattern matching functions like
reFind()andreMatch(). But, nothing that compares to thePatternandMatcherclasses under the hood (in the Java layer). I just need to create a nice wrapper that made the methods a bit easier to use.Awesome. I shall be adding this to my library, if that's OK?
BTW. Did you see I managed to find a solution to our 'object as a value' in a checkbox problem. It's a little 'round the houses', but it works:
https://codesandbox.io/embed/jnxn34o41w?codemirror=1
I've had a look at your JRegEx CFC. It is amazing. Really powerful stuff. Just one tiny little observation. I know you are really busy, but when you have a spare moment, it would be so great, if you could add the output to your examples.
Maybe, it's already there, and it's just my stupid mobile phone, not being able to scroll the example container?!?
Although, the documentation is very thorough, I am never entirely sure, whether I have fully understood an example, unless, I can see the output created by a function.
Cheers!
@Charles,
I'm trying to wrap my head around your
FormControlstuff, but I don't yet have the instinct for the reactive-forms model. I see that you're creating anew FormControl()and then.... associating it to the DOM using theformControlName. Gonna need to let that sink into my head.Re:
JRegEx, you are correct -- there is no output. That would be easy enough to add to the ReadMe. I'll put that on my list.@All,
After going back and forth on the idea of embedding widgets .... I think I might just end up putting the plain HTML right in the markdown. I still enjoy the idea of creating a separation of concerns; but, I could already feel that I wasn't going to be able to consistently create an abstraction. The thing that tripped-me-up was the fenced-code blocks. I want to wrap my code-blocks in a container; but, if I did that with something like a
<InvalidTag>tag, it would prevent the fenced-code-block from being parsed. At that point, I realized that I'd likely to have to wrap my code-block in a<div>.Still trying to noodle on all of this; but, just wanted to share that I might be wavering on the concept.
Ha ha, ColdFusion replaced my "script" tag with an "InvalidTag". That's the native XSS protection. Oh well.