Conditional Router Outlets Mostly Work In Angular 4.4.0-RC.0
I started digging into the Angular 2 Router a year ago when Angular 2 was still just a release-candidate (RC). At the time, the in-built Router had a fatal flaw: it wouldn't allow <router-outlet> directives to be conditionally rendered in the DOM (Document Object Model). This was a show-stopper for a complex user interface (UI) like InVision App. To get around this, I switched over to the ngRx Router, which worked beautifully. Until the ngRx Router was end-of-lifed. At which point I just gave up and stopped experimenting with routing. Now, over a year later, I wanted to check back in with the Angular 4 Router to see if the situation had improved. And, thankfully it has. Mostly. With Angular 4.4.0, conditional Router outlets now mostly work. "Mostly" in that they are allowed; but, "mostly" in that they do break in certain circumstances.
Run this demo in my JavaScript Demos project on GitHub.
To be clear, when I say "conditional router outlet", what I mean is that I have a nested set of Views in which the inner View's <router-outlet> directive is being rendered based on the conditions of the outer View's model. Typically through something like ngIf or ngSwitch:
<div *ngIf="isLoaded" class="sub-detail">
<p>
Some dynamic content BEFORE sub-detail.
</p>
<router-outlet></router-outlet>
<p>
Some dynamic content AFTER sub-detail.
</p>
</div>
As you can see here, the inner <router-outlet> will only be rendered in the DOM if the outer view's isLoaded model is True. In Angular 2, this approach would simply error-out and nothing would load. In Angular 4, however, it mostly works. If you conditionally include a nested router outlet, Angular 4 will lazily instantiate and render the view component. The problem is, Angular still has trouble destroying a partially-rendered view component tree. And, there are some increased complexities around RxJS subscriptions and the view component life-cycle.
To explore the new constraints of conditionally rendered router outlets, I created a simple Angular application that has a Parent Component that renderes a nested Child Component. The application will be driven by just a home route (empty path) and a single nested parent/child route:
// Import the core angular services.
import { BrowserModule } from "@angular/platform-browser";
import { NgModule } from "@angular/core";
import { RouterModule } from "@angular/router";
import { Routes } from "@angular/router";
// Import the application components and services.
import { AppComponent } from "./app.component";
import { ChildComponent } from "./child.component";
import { ParentComponent } from "./parent.component";
// ----------------------------------------------------------------------------------- //
// ----------------------------------------------------------------------------------- //
var routes: Routes = [
{
path: "parent/:id",
component: ParentComponent,
children: [
{
path: "child/:id",
component: ChildComponent
}
]
},
{
path: "**",
redirectTo: "/"
}
];
// ----------------------------------------------------------------------------------- //
// ----------------------------------------------------------------------------------- //
@NgModule({
bootstrap: [
AppComponent
],
imports: [
BrowserModule,
RouterModule.forRoot(
routes,
{
// Tell the router to use the HashLocationStrategy.
useHash: true
}
)
],
declarations: [
AppComponent,
ChildComponent,
ParentComponent
],
providers: [
// CAUTION: We don't need to specify the LocationStrategy because we are setting
// the "useHash" property in the Router module above.
// --
// {
// provide: LocationStrategy,
// useClass: HashLocationStrategy
// }
]
})
export class AppModule {
// ...
}
As you can see, there's just two routes:
- /
- /parent/:id/child/:id
But, only the nested route has any associated components; so, the home route will simply render the App component without any router-outlet.
The App component provides the navigation so that we can jump from route to route:
// Import the core angular services.
import { Component } from "@angular/core";
import { Event as NavigationEvent } from "@angular/router";
import { NavigationEnd } from "@angular/router";
import { Router } from "@angular/router";
// ----------------------------------------------------------------------------------- //
// ----------------------------------------------------------------------------------- //
@Component({
selector: "my-app",
styleUrls: [ "./app.component.css" ],
template:
`
<h2>
App Routing Component
</h2>
<ul>
<li>
<a routerLink="/">Home</a>
<strong *ngIf="activated.home">«—Selected</strong>
</li>
<li>
<a routerLink="/parent/p1/child/p1-c1">Route: /parent/p1/child/p1-c1</a>
<strong *ngIf="activated.p1c1">«—Selected</strong>
</li>
<li>
<a routerLink="/parent/p1/child/p1-c2">Route: /parent/p1/child/p1-c2</a>
<strong *ngIf="activated.p1c2">«—Selected</strong>
</li>
<li>
<a routerLink="/parent/p2/child/p2-c1">Route: /parent/p2/child/p2-c1</a>
<strong *ngIf="activated.p2c1">«—Selected</strong>
</li>
<li>
<a routerLink="/parent/p2/child/p2-c2">Route: /parent/p2/child/p2-c2</a>
<strong *ngIf="activated.p2c2">«—Selected</strong>
</li>
</ul>
<router-outlet></router-outlet>
<hr />
<p>
<strong>"Mostly" work?</strong> If you click into p1-c1 and let it load.
Then, you click into p2-c2 and then hit your back button (before it loads),
you will see that it breaks with the error
<code>"Cannot read property 'component' of null"</code>.
This error goes away if the router-outlet is always on the page
(ie, not in an ngIf template).
</p>
`
})
export class AppComponent {
public activated: {
home: boolean;
p1c1: boolean;
p1c2: boolean;
p2c1: boolean;
p2c2: boolean;
};
private router: Router;
// I initialize the app component.
constructor( router: Router ) {
this.router = router;
this.activated = {
home: false,
p1c1: false,
p1c2: false,
p2c1: false,
p2c2: false
};
// Listen for routing events so we can update the activated route indicator
// as the user navigates around the application.
this.router.events.subscribe(
( event: NavigationEvent ) : void => {
if ( event instanceof NavigationEnd ) {
this.activated.home = this.router.isActive( "/", true );
this.activated.p1c1 = this.router.isActive( "/parent/p1/child/p1-c1", true );
this.activated.p1c2 = this.router.isActive( "/parent/p1/child/p1-c2", true );
this.activated.p2c1 = this.router.isActive( "/parent/p2/child/p2-c1", true );
this.activated.p2c2 = this.router.isActive( "/parent/p2/child/p2-c2", true );
}
}
);
}
}
There's not much going on in the App component. But, we can see that it provides 5 routerLink directives:
- /
- /parent/p1/child/p1-c1
- /parent/p1/child/p1-c2
- /parent/p2/child/p2-c1
- /parent/p2/child/p2-c2
The most important thing to see here is that the application provides a way to jump from one deeply nested route to another, without having to navigate back up a set of views. Before you dismiss this as an unrealistic example, remember that this is essentially what you can do using browser Bookmarks; or by copy-pasting a link from a friend; or by a set of "related item" links in the application logic; or by many other means.
To think that you can't jump from one deeply-nested view to another is simply an unrealistic constraint.
That said, let's look at the ParentComponent, which will conditionally render the ChildComponent's router-outlet:
// Import the core angular services.
import { ActivatedRoute } from "@angular/router";
import { Component } from "@angular/core";
import { ParamMap } from "@angular/router";
import { Subscription } from "rxjs/Subscription";
// Import these modules for their side-effects.
import "rxjs/add/operator/delay";
// ----------------------------------------------------------------------------------- //
// ----------------------------------------------------------------------------------- //
@Component({
selector: "my-parent",
styleUrls: [ "./parent.component.css" ],
template:
`
<h3>
Parent Routing Component
</h3>
<ng-template [ngIf]="isLoading">
<p>
<em>Loading parent data...</em>
</p>
</ng-template>
<!--
Notice that the ROUTER OUTLET is not always part of the active DOM. It is
only rendered once the surrounding parent component data has loaded. Notice
also that it is nested inside the layout and CANNOT be factored-out into a
separate location in the DOM.
-->
<ng-template [ngIf]="! isLoading">
<div class="view">
<p>
Parent data is <strong>loaded</strong> (for ID: {{ id }}).
</p>
<router-outlet></router-outlet>
</div>
</ng-template>
`
})
export class ParentComponent {
public id: string;
public isLoading: boolean;
private paramSubscription: Subscription;
private timer: number;
// I initialize the parent component.
constructor( activatedRoute: ActivatedRoute ) {
console.warn( "Parent component initialized." );
this.id = "";
this.isLoading = true;
this.timer = null;
// While the Parent Component is rendered, it's possible that the :id parameter
// in the route will change. As such, we want to subscribe to the activated route
// so that we can load the new data as the :id value changes (this will also give
// us access to the FIRST id value as well).
// --
// NOTE: If you only wanted the initial value of the parameter, you could use the
// route snapshot - activatedRoute.snapshot.paramMap.get( "id" ).
this.paramSubscription = activatedRoute.paramMap.subscribe(
( params: ParamMap ) : void => {
console.log( "Parent ID changed:", params.get( "id" ) );
this.isLoading = true;
// Simulate loading the data from some external service.
this.timer = this.timer = setTimeout(
() : void => {
this.id = params.get( "id" );
this.isLoading = false;
},
2000
);
}
);
}
// ---
// PUBLIC METHODS.
// ---
// I get called once when the component is being unmounted.
public ngOnDestroy() : void {
console.warn( "Parent component destroyed." );
// When the Parent component is destroyed, we need to stop listening for param
// changes so that we don't continually load data in the background.
// --
// CAUTION: The Angular documentation indicates that you don't need to do this
// for ActivatedRoute observables; however, if you log the changes, you will see
// that the observables don't get killed when the route component is destroyed.
this.paramSubscription.unsubscribe();
clearTimeout( this.timer );
}
}
Again, there's not very much going on in this application. When the ParentComponent loads, we subscribe to the paramMap to start observing :id values. And, when an :id value comes in, we create a Timer to simulate network latency. Then, while we're "fetching" remote data, we omit the <router-outlet> from the DOM via the isLoading model. This means that there will be a 2-second delay between the rendering of the ParentComponent and the rendering of the ChildComponent.
The ChildComponent is basically a copy of the ParentComponent with a few details changed, not the least of which is that it has no nested router-outlet:
// Import the core angular services.
import { ActivatedRoute } from "@angular/router";
import { Component } from "@angular/core";
import { ParamMap } from "@angular/router";
import { Subscription } from "rxjs/Subscription";
// Import these modules for their side-effects.
import "rxjs/add/operator/delay";
// ----------------------------------------------------------------------------------- //
// ----------------------------------------------------------------------------------- //
@Component({
selector: "my-child",
styleUrls: [ "./child.component.css" ],
template:
`
<h4>
Child Routing Component
</h4>
<ng-template [ngIf]="isLoading">
<p>
<em>Loading child data...</em>
</p>
</ng-template>
<ng-template [ngIf]="! isLoading">
<div class="view">
<p>
Child data is <strong>loaded</strong> (for ID: {{ id }}).
</p>
</div>
</ng-template>
`
})
export class ChildComponent {
public id: string;
public isLoading: boolean;
private paramSubscription: Subscription;
private timer: number;
// I initialize the child component.
constructor( activatedRoute: ActivatedRoute ) {
console.warn( "Child component initialized." );
this.id = "";
this.isLoading = true;
this.timer = null;
// While the Child Component is rendered, it's possible that the :id parameter
// in the route will change. As such, we want to subscribe to the activated route
// so that we can load the new data as the :id value changes (this will also give
// us access to the FIRST id value as well).
// --
// NOTE: If you only wanted the initial value of the parameter, you could use the
// route snapshot - activatedRoute.snapshot.paramMap.get( "id" ).
this.paramSubscription = activatedRoute.paramMap
// TIMING HACK: We need a tick-delay to allow ngOnDestroy() to fire first
// (before our subscribe function is invoked) if the route changes in such a
// way that it has to destroy the Child component before it re-renders it
// (such as navigating from "p1-c1" to "p2-c1).
.delay( 0 )
.subscribe(
( params: ParamMap ) : void => {
console.log( "Child ID changed:", params.get( "id" ) );
this.isLoading = true;
// Simulate loading the data from some external service.
this.timer = setTimeout(
() : void => {
this.id = params.get( "id" );
this.isLoading = false;
},
2000
);
}
)
;
}
// ---
// PUBLIC METHODS.
// ---
// I get called once when the component is being unmounted.
public ngOnDestroy() : void {
console.warn( "Child component destroyed." );
// When the Child component is destroyed, we need to stop listening for param
// changes so that we don't continually load data in the background.
// --
// CAUTION: The Angular documentation indicates that you don't need to do this
// for ActivatedRoute observables; however, that seems to ONLY BE TRUE if you
// navigate to a DIFFERENT ROUTE PATTERN. If you remain in the ROUTE PATTERN,
// but do so in a way that this component is destroyed, the Router WILL NOT
// automatically unsubscribe from the Observable (ex, going from "p1-c1" to
// "p2-c2"). As such, it is a best practice to ALWAYS unsubscribe from changes,
// regardless of what the documentation says.
this.paramSubscription.unsubscribe();
clearTimeout( this.timer );
}
}
As you can see, the ChildComponent is doing the same thing as the ParentComponent - we're subscribing to the paramMap and then using a Timer to simulate network latency for the load. And, as it stands, this mostly works. If you load this app and click from the default Home view to one of the nested child views, the application incrementally renders the nested views:
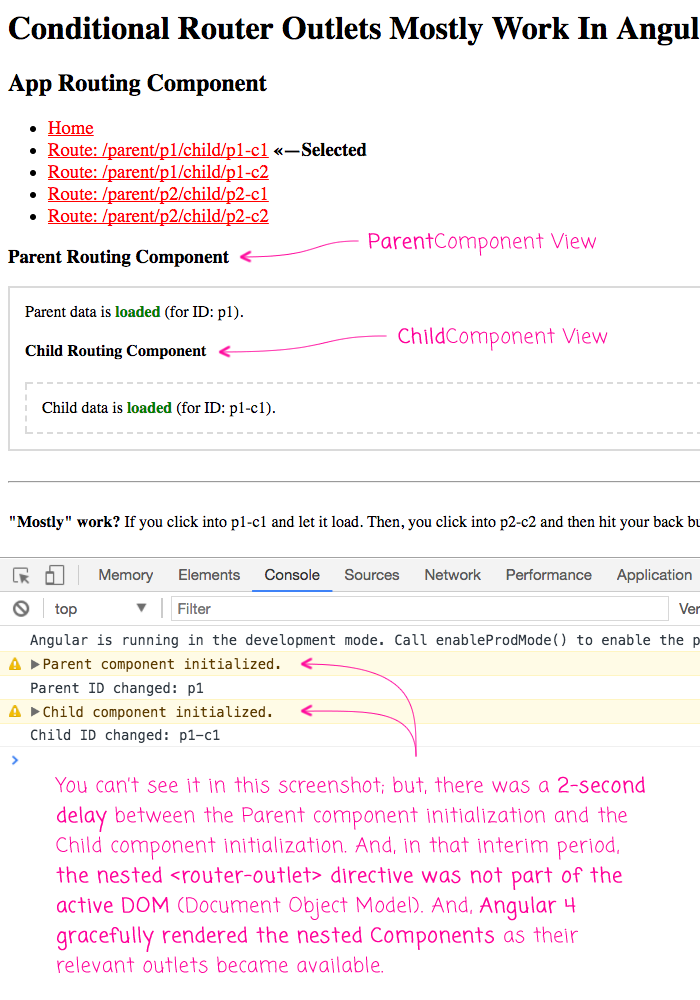
This is pretty exciting! This is huge progress over the router in Angular 2 RC. However, it's not perfect. If you go to the p1-c1 view, let it render the nested views, then click over to the p2-c1 view, and click your browser's back button before p2-c1 has a chance to full render, you get an Angular error:
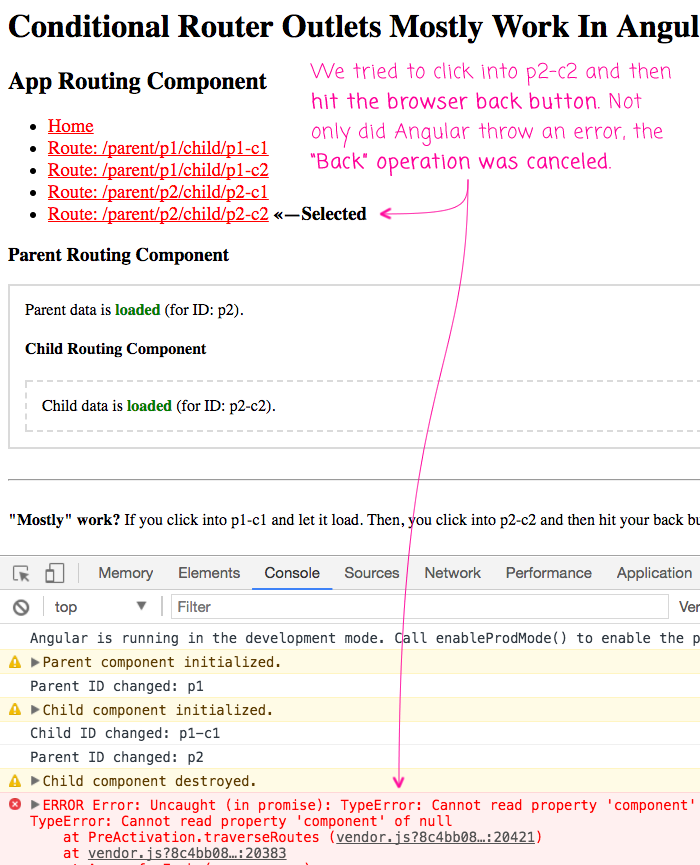
As you can see, not only did our Back-button operation get ignored but Angular 4 throws the error:
Cannot read property 'component' of null
My theory here is that when going from p1-c1 to p2-c2, Angular sees that the route pattern hasn't changed, only the parameters have. As such, it tries to traverse the component tree running guard statements. Only, our ChildComponent hasn't been initialized yet do to the 2-second network latency simulation. As such, the ChildComponent is still null in the component tree during the traversal.
This is clearly a big problem. But, the saving grace of this use-case is that the application is still usable even after the error is thrown. It's not a catastrophic failure from the user's perspective; just an unfortunate user experience.
Now, this is not the only problem with conditionally rendered router-outlets. Another issue is that the Angular documentation doesn't yet account for being able to jump from one nested view to another nested view. If you look at how the Angular documentation describes RxJS in the Router, it makes it sound like you don't have to care:
When subscribing to an observable in a component, you almost always arrange to unsubscribe when the component is destroyed.
There are a few exceptional observables where this is not necessary. The ActivatedRoute observables are among the exceptions.
The ActivatedRoute and its observables are insulated from the Router itself. The Router destroys a routed component when it is no longer needed and the injected ActivatedRoute dies with it.
This is incorrect. Or, perhaps, it's not fully correct. If you look at my ChildComponent, you will see in the ngOnDestroy() life-cycle hook, I am unsubscribing from the paramMap observable. This is required - it's not just a "best practice." If I omit that line, and leave it up to Angular Router to manage the subscription, then jumping from one nested view to another nested view will leave those subscriptions in-tact even though the ChildComponent gets destroyed (while the ParentComponent is loading data). This will end up compounding the number of data-load events that your application has to perform.
I clearly demonstrate this issue in the video. But, if I comment-out the .unsubscribe() line and then jump back and forth between p1-c1 and p2-c1, I get the following output:
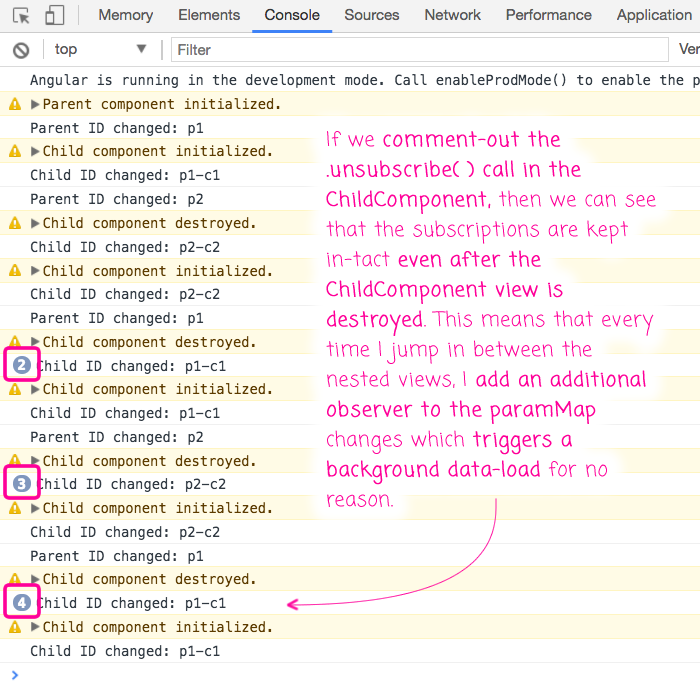
As you can see, the paramMap subscribers are never unsubscribed even as the ChildComponent instances are destroyed. As such, more and more subscribers react to the paramMap events, trigger more and more data loading in the background.
Always unsubscribe your subscriptions!
The last issue that I ran into involves the timing of the paramMap events and the destruction of the ChildComponent view. But, I believe this may be related to the previous issue. If you look in my paramMap subscription, you will see that I have a .delay(0) RxJS operator before I subscribe to the :id changes. This delay is required because, otherwise, when I jump from p1-c1 to p2-c1, the to-be-destroyed ChildComponent receives one last :id change right before the component is destroyed. This causes unnecessary data-loading in the background.
To this in action, I'll comment-out the .delay(0) operator and jump back and forth between two children that have different parents:
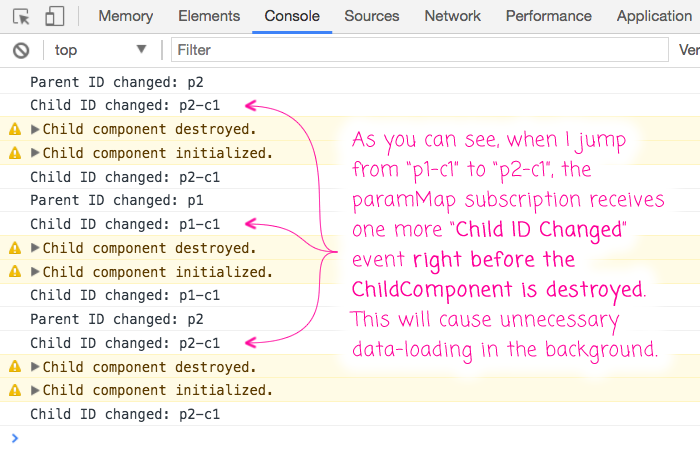
As you can see, when I jump from one nested child route to another nested child route, the ChildComponent receives one more paramMap event right before the ChildComponent is destroyed (due to the conditional rendering within the ParentComponent). In a real-world scenario, this would likely trigger an unnecessary data-load. As such, I added the .delay(0) to make sure my subscriber would be triggered asynchronously, giving my ngOnDestroy() life-cycle hook a chance to unsubscribe from the paramMap Observable before the event is propagated.
The Angular 4 Router is getting much closer to being feature-complete. With conditional router-outlets mostly working, I'm excited to see that the core Router is now a potential candidate for a complex, nested user interface (such as that presented in InVision App). Hopefully they'll have this rounded out in the next few releases!
Want to use code from this post? Check out the license.

Reader Comments
Did they remove named outlets?
When i try to put the heros view in another outlet like you described i am have errors.
{
path: 'heroes',
component: HeroesComponent,
outlet: 'test'
}
<router-outlet></router-outlet>
<router-outlet name="test"></router-outlet>
@Bert,
I am just playing around with named-outlets right now, and I'm also having a lot of trouble getting it to work. It keeps telling me that it can't match any route. I'm not using the Tour of Heroes; so, it might be an issue on my end. But certainly, I am having trouble getting it to work.
@Bert,
Just to circle back on this, I have been using named-outlets in my R&D and they work fairly well. A few quirks; but, generally speaking, I have them working.
@All,
It looks like someone has a PR that would actually fix the error I was seeing:
https://github.com/angular/angular/pull/19374
... hoping that gets fixed soon :D
hi,
awesome read. keep it up.
Thank You for such an awesome post, Learnt alot from this post, I will keep visiting your blog on daily basis to learn more.
@Sovof, @Aman,
Very cool -- so happy to hear that this stuff has been useful :D